
 如圖,一次函數y=-x-1與反比例函數y=$\frac{m}{x}$在第二象限交于點A,一次函數y=-x-1與坐標軸分別交于B、C兩點,連結AO,若tan∠AOB=$\frac{1}{3}$.
如圖,一次函數y=-x-1與反比例函數y=$\frac{m}{x}$在第二象限交于點A,一次函數y=-x-1與坐標軸分別交于B、C兩點,連結AO,若tan∠AOB=$\frac{1}{3}$.分析 (1)設出A點的坐標為(a,b)(a<0),結合題意,由于tan∠AOB=$\frac{1}{3}$,易得出3b+a=0;又因為A點一次函數圖象上,即有-a-1=b,兩方程聯立即可得出A點的坐標,代入反比例函數解析式中,得k,便可得出反比例函數解析式;
(2)利用一次函數解析式,得出C點的坐標,易得OC的長,結合(1),可得出點A到y軸的距離為A點橫坐標的絕對值,代入三角形面積公式,即可得出△AOC的面積.然后設出D的坐標,根據三角形的面積公式求解.
解答 解:(1)設A(a,b),結合題意,
-a-1=b,
又tan∠AOB=$\frac{1}{3}$,
即有3b+a=0;
可得出a=$\frac{3}{2}$,b=$\frac{1}{2}$;
即A($\frac{3}{2}$,$\frac{1}{2}$),
代入反比例函數解析式中,有$\frac{1}{2}$=$\frac{m}{-\frac{3}{2}}$,
得m=$\frac{3}{4}$,
故反比例函數解析式為:y=$\frac{3}{4x}$;
(2)因為一次函數y=-x-1與坐標軸交C點,
令x=0,得y=-1,
即C(0,-1);
所以OC=1;
又∵A(-$\frac{3}{2}$,$\frac{1}{2}$),
即點A到x軸的距離為$\frac{1}{2}$,
因為一次函數y=-x-1與x軸交B點,
令y=0,得x=-1,
即B(-1,0);
則OB=1,
所以S△AOC=$\frac{1}{2}$OB•$\frac{1}{2}$+$\frac{1}{2}$OB•OC=$\frac{3}{4}$.
設D的橫坐標是(m,0),
則BD=|m+1|.
則$\frac{1}{2}$|m+1|×1=$\frac{3}{4}$,
解得:m=$\frac{1}{2}$或-$\frac{5}{2}$.
則D的坐標是($\frac{1}{2}$,0)或(-$\frac{5}{2}$,0).
點評 本題主要考查了反比例函數和一次函數的綜合應用,以及三角形的面積的求法等知識點,題目較為簡單,適合學生平時的練習使用.


科目:初中數學 來源: 題型:解答題
| 月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
| 錢數變化 | +300 | +220 | -150 | -100 | +330 | +200 | +280 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
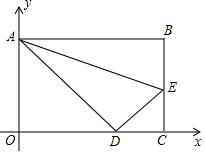 如圖,在矩形OABC中,點C在x軸上,點A在y軸上,且OA,OC的長分別是一元二次方程x2-18x+80=0的兩個根(OA<OC),點E在BC上,將△ABE沿AE折疊,使點B落在OC上.
如圖,在矩形OABC中,點C在x軸上,點A在y軸上,且OA,OC的長分別是一元二次方程x2-18x+80=0的兩個根(OA<OC),點E在BC上,將△ABE沿AE折疊,使點B落在OC上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知二次函數y=-x2+2x+m圖象過點A(3,0),與y軸交于點B
如圖,已知二次函數y=-x2+2x+m圖象過點A(3,0),與y軸交于點B查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com