Question

14．已知，等腰Rt△ABC，∠BAC=Rt∠，在直角邊AB的左側作直線AP，點B關于直線AP的對稱點為E，連結BE，CE，其中CE交直線AP于點F．
（1）依題意，在圖1中補全示意圖；當∠PAB=18°時，求∠ACF的度數；
（2）當0°＜∠PAB＜45°時，利用圖1，求證：∠PAB+∠ACE=45°；
（3）如圖2，若45°＜∠PAB＜90°，用等式表示線段AB，FE，FC之間的數量關系，并證明．

Answer 1

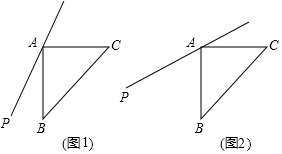
分析 （1）由軸對稱的性質和等腰三角形的性質得出∠EAP=∠PAB=18°，得出∠EAC=126°，證出AE=AC，由等腰三角形的性質和三角形內角和定理即可得出結果；
（2）由（1）得：∠EAP=∠PAB，∠AEC=∠ACE，由三角形內角和定理即可得出結論；
（3）作CG⊥AP于G，由AAS證明△ACG≌△BAM，得出CG=AM，證出點A是△BCE的外接圓圓心，由圓周角定理得出∠BEC=$\frac{1}{2}$∠BAC=45°，得出△EFM和△CFG是等腰直角三角形，由勾股定理即可得出結論．

解答 （1）解：如圖1所示：
∵由軸對稱的性質得：AE=AC，BM=EM，AM⊥BE，∠AME=∠BMA=90°，
∴∠EAP=∠PAB=18°，
∴∠EAC=90°+2×16°=126°，
∵△ABC是等腰直角三角形，
∴AB=AC，
∴AE=AC，
∴∠ACF=∠AEC=$\frac{1}{2}$（180°-126°）=27°；
（2）證明：由（1）得：∠EAP=∠PAB，∠AEC=∠ACE，
∵∠AEC+∠ACE+∠EAC=180°，
∴∠AEC+∠ACE+2∠PAB=90°，
即2∠ACE+2∠PAB=90°，
∴∠PAB+∠ACE=45°；
（3）解：EF²+CF²=2AB²，理由如下：
如圖2所示：作CG⊥AP于G，
則∠AGC=∠BMA=90°，
∵∠BAC=90°，
∴∠GAC=∠MBA，
在△ACG和△BAM中，$\left\{\begin{array}{l}{∠GAC=∠MBA}&{\;}\\{∠∠BMA}&{\;}\\{AC=BA}&{\;}\end{array}\right.$，
∴△ACG≌△BAM（AAS），
∴CG=AM，
∵AB=AC=AE，
∴點A是△BCE的外接圓圓心，
∴∠BEC=$\frac{1}{2}$∠BAC=45°，
∴∠CFG=∠EFM=45°，
∴△EFM和△CFG是等腰直角三角形，
∴EF²=2EM²，CF²=2CG²，
∵AB²=AM²+BM²，
∴EF²+CF²=2AB²．

點評 本題是三角形綜合題目，考查了軸對稱的性質、等腰三角形的性質、全等三角形的判定與性質、三角形內角和定理、圓周角定理、勾股定理等知識；本題綜合性強，有一定難度．