
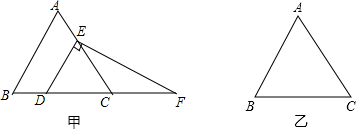
分析 (1)利用平行線判斷出△EDC是等邊三角形,得出CD=CE,∠CDE=∠CED=60°,再用直角和三角形的外角即可得出CE=CF,即可;
(2)利用含30°的直角三角形的性質(zhì)即可得出結(jié)論;
(3)同(1)的方法直接證明.
解答 解:(1)∵△ABC是等邊三角形,
∴∠B=∠ACB=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∴△EDC是等邊三角形,
∴CD=CE,∠CDE=∠CED=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠CEF=30°,
∵∠F=∠ACB-∠CEF=60°-30°=30°,
∴CE=CF,
∴CD=CF
(2)∵△EDC是等邊三角形
∴DE=DC=2,
在Rt△DEF中,∵∠DEF=90°,DE=2,
∴DF=2DE=4,
∴EF=$\sqrt{D{F}^{2}-D{E}^{2}}$=2$\sqrt{3}$,
(3)CD=CF還成立,
理由:如圖乙,
∵△ABC是等邊三角形,
∴∠B=∠ACB=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∴△EDC是等邊三角形,
∴CD=CE,∠CDE=∠CED=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠CEF=30°,
∵∠DFE=∠DCE-∠CEF=60°-30°=30°,
∴CE=CF,
∴CD=CF.
點評 此題是三角形綜合題,主要考查了等邊三角形的判定和性質(zhì),三角形的外角的性質(zhì),勾股定理,判斷出△EDC是等邊三角形是解本題的關(guān)鍵.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案 單元加期末復(fù)習(xí)先鋒大考卷系列答案
單元加期末復(fù)習(xí)先鋒大考卷系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
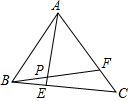 如圖,△ABC中,E是BC上的一點,F(xiàn)是AC上一點,且3BE=BC,4CF=AF,AE、BF交于P點,如果△ABP的面積是30平方厘米,求△ABC的面積$\frac{120}{11}$.
如圖,△ABC中,E是BC上的一點,F(xiàn)是AC上一點,且3BE=BC,4CF=AF,AE、BF交于P點,如果△ABP的面積是30平方厘米,求△ABC的面積$\frac{120}{11}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
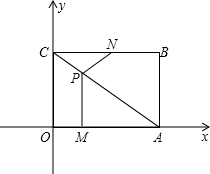 如圖,平面直角坐標系中,四邊形OABC為矩形,點A,B的坐標分別為(4,0),(4,3),動點M,N分別從O,B同時出發(fā).以每秒1個單位的速度運動.其中,點M沿OA向終點A運動,點N沿BC向終點C運動.其中,點M沿OA向終點A運動,點N沿BN向終點C運動.過點M作MP⊥OA,交AC于P,連接NP,設(shè)M、N運動的時間為t秒(0<t<4).
如圖,平面直角坐標系中,四邊形OABC為矩形,點A,B的坐標分別為(4,0),(4,3),動點M,N分別從O,B同時出發(fā).以每秒1個單位的速度運動.其中,點M沿OA向終點A運動,點N沿BC向終點C運動.其中,點M沿OA向終點A運動,點N沿BN向終點C運動.過點M作MP⊥OA,交AC于P,連接NP,設(shè)M、N運動的時間為t秒(0<t<4).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
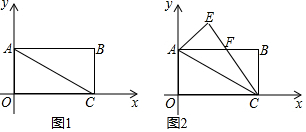
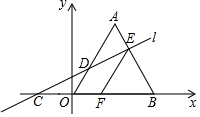 如圖,在平面直角坐標系中,△AOB是邊長為6的等邊三角形,直線l與x軸、OA、AB分別交于點C、D、E,OC=AE.過點E作EF∥OA,交x軸于點F.
如圖,在平面直角坐標系中,△AOB是邊長為6的等邊三角形,直線l與x軸、OA、AB分別交于點C、D、E,OC=AE.過點E作EF∥OA,交x軸于點F.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
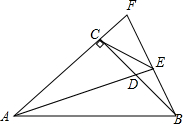 如圖,在△ABC中,∠ACB=90°,AC=BC,AD為△ABC的角平分線,過點B作AD的垂線,分別交AD、AC的延長線于E、F兩點,連接CE.
如圖,在△ABC中,∠ACB=90°,AC=BC,AD為△ABC的角平分線,過點B作AD的垂線,分別交AD、AC的延長線于E、F兩點,連接CE.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com