
| A. | -$\frac{7}{4}$ | B. | $\sqrt{3}$或-$\sqrt{3}$ | C. | 2或-$\sqrt{3}$ | D. | 2或-$\sqrt{3}$或-$\frac{7}{4}$ |
分析 求出二次函數(shù)對稱軸為直線x=m,再分m<-2,-2≤m≤1,m>1三種情況,根據(jù)二次函數(shù)的增減性列方程求解即可.
解答 解:二次函數(shù)對稱軸為直線x=m,
①m<-2時,x=-2取得最大值,-(-2-m)2+m2+1=4,
解得m=-$\frac{7}{4}$,不合題意,舍去;
②-2≤m≤1時,x=m取得最大值,m2+1=4,
解得m=±$\sqrt{3}$,
∵m=$\sqrt{3}$不滿足-2≤m≤1的范圍,
∴m=-$\sqrt{3}$;
③m>1時,x=1取得最大值,-(1-m)2+m2+1=4,
解得m=2.
綜上所述,m=2或-$\sqrt{3}$時,二次函數(shù)有最大值4.
故選:C.
點評 本題考查了二次函數(shù)的最值,熟悉二次函數(shù)的性質及圖象是解題的關鍵.


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數(shù)學 來源: 題型:解答題
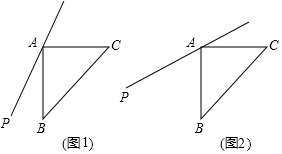
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
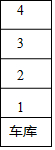 甲、乙兩人同在如圖所示的地下車庫等電梯,兩人到1至4層的任意一層出電梯,
甲、乙兩人同在如圖所示的地下車庫等電梯,兩人到1至4層的任意一層出電梯,查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
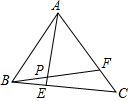 如圖,△ABC中,E是BC上的一點,F(xiàn)是AC上一點,且3BE=BC,4CF=AF,AE、BF交于P點,如果△ABP的面積是30平方厘米,求△ABC的面積$\frac{120}{11}$.
如圖,△ABC中,E是BC上的一點,F(xiàn)是AC上一點,且3BE=BC,4CF=AF,AE、BF交于P點,如果△ABP的面積是30平方厘米,求△ABC的面積$\frac{120}{11}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com