
 如圖,在四邊形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,則下列結論:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四邊形ABCD的面積為31;⑤BD=2$\sqrt{41}$.正確的是②③④⑤.
如圖,在四邊形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,則下列結論:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四邊形ABCD的面積為31;⑤BD=2$\sqrt{41}$.正確的是②③④⑤. 分析 根據勾股定理及其逆定理可得AC2+CD2=DA2知∠ACD=90°,即AC⊥CD,故①錯誤,②正確;根據正切函數的定義可判斷③;根據四邊形ABCD的面積為S△ABC+S△ACD可判斷④;作DM⊥BC,交BC延長線于M,連接AC,由勾股定理得出AC2=AB2+BC2=25,求出AC2+CD2=AD2,由勾股定理的逆定理得出△ACD是直角三角形,∠ACD=90°,證出∠ACB=∠CDM,得出△ABC∽△CMD,由相似三角形的對應邊成比例求出CM=2AB=6,DM=2BC=8,得出BM=BC+CM=10,再由勾股定理求出BD即可判斷⑤.
解答 解:∵∠ABC=90°,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
在△ACD中,∵CD=10,DA=5$\sqrt{5}$,
∴AC2+CD2=25+100=125=DA2,
∴∠ACD=90°,即AC⊥CD,故①錯誤,②正確;
在Rt△ACD中,tan∠DAC=$\frac{CD}{AC}$=$\frac{10}{5}$=2,故③正確;
S四邊形ABCD=S△ABC+S△ACD
=$\frac{1}{2}$AB•BC+$\frac{1}{2}$AC•CD
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×10
=31,
故④正確;
作DM⊥BC,交BC延長線于M,如圖所示:
則∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC2=AB2+BC2=25,
∵CD=10,AD=5$\sqrt{5}$,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
∴△ABC∽△CMD,
∴$\frac{AB}{CM}$=$\frac{1}{2}$,
∴CM=2AB=6,DM=2BC=8,
∴BM=BC+CM=10,
∴BD=$\sqrt{B{M}^{2}+D{M}^{2}}$=2$\sqrt{41}$,故⑤正確;
故答案為:②③④⑤.
點評 本題考查了相似三角形的判定與性質、勾股定理、勾股定理的逆定理;熟練掌握相似三角形的判定與性質,證明由勾股定理的逆定理證出△ACD是直角三角形是解決問題的關鍵.


科目:初中數學 來源: 題型:填空題
 如圖,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一點M、N使BM+MN的值最小,則這個最小值為2$\sqrt{3}$.
如圖,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一點M、N使BM+MN的值最小,則這個最小值為2$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,把一張三角形紙片ABC沿中位線DE剪開后,在平面上將△ADE繞著點E順時針旋轉180°,點D運動到點F的位置,則S△ADE:S四邊形DBCF是1:4.
如圖,把一張三角形紙片ABC沿中位線DE剪開后,在平面上將△ADE繞著點E順時針旋轉180°,點D運動到點F的位置,則S△ADE:S四邊形DBCF是1:4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
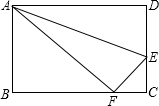 如圖,在長方形ABCD(長方形四個角都是直角,并且對邊相等)中,DC=5,點E在DC上,沿AE折疊△ADE,使D點與BC邊上的點F重合,△ABF的面積是30,求DE的長.
如圖,在長方形ABCD(長方形四個角都是直角,并且對邊相等)中,DC=5,點E在DC上,沿AE折疊△ADE,使D點與BC邊上的點F重合,△ABF的面積是30,求DE的長.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com