
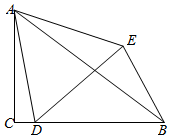
 在Rt△ACB中,∠ACB=90°,點D在邊BC上,連接AD,以點D為頂點,AD為一邊作等邊△ADE,連接BE,若BC=7,BE=4,∠CBE=60°,則∠EAB的正切值為$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,點D在邊BC上,連接AD,以點D為頂點,AD為一邊作等邊△ADE,連接BE,若BC=7,BE=4,∠CBE=60°,則∠EAB的正切值為$\frac{2\sqrt{3}}{11}$. 分析 過點D作DF⊥BE于點F,由等邊三角形的性質結合角的計算即可得出AD=DE、∠ADC=∠DEF,利用全等三角形的判定定理AAS即可證出△ACD≌△DFE,由此即可得出AC=DF、CD=FE,由BC=7,BE=4,可設CD=FE=x,則:BD=7-x,BF=4-x.根據BD=2BF即可得出關于x的方程,解之即可得出x的值,再根據勾股定理即可得出AD、AB的長度,過點E作EG⊥AB于點G,由勾股定理可得AE2-AG2=BE2-BG2,代入數據可得出AG、EG的長度,利用正切的定義即可得出∠EAB的正切值.
解答 解:過點D作DF⊥BE于點F,如圖1所示.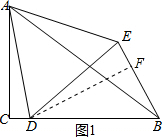
∵△ADE是等邊三角形,
∴AD=DE=AE,∠ADE=60°.
∵∠CBE=60°,
∴∠ADE=∠DBF=60°,
∴BD=2BF,∠ADC+∠BDE=∠DEF+∠BDE=120°,
∴∠ADC=∠DEF.
在△ACD和△DFE中,$\left\{\begin{array}{l}{∠ADC=∠DEF}\\{∠ACD=∠DFE=90°}\\{AD=DE}\end{array}\right.$,
∴△ACD≌△DFE(AAS),
∴AC=DF,CD=FE.
∵BC=7,BE=4,
∴設CD=FE=x,則:BD=7-x,BF=4-x.
∵BD=2BF,
∴7-x=2(4-x),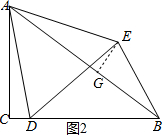
∴x=1.
∴CD=FE=1,BD=6,BF=3.
∴AC=DF=$\sqrt{3}$BF=3$\sqrt{3}$.
由勾股定理可得:AD=DE=AE=$\sqrt{A{C}^{2}+C{D}^{2}}$=2$\sqrt{7}$,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{19}$.
過點E作EG⊥AB于點G,如圖2所示.
∵AE2-AG2=BE2-BG2,
∴$(2\sqrt{7})^{2}$-AG2=42-$(2\sqrt{19}-AG)^{2}$,
∴AG=$\frac{22\sqrt{19}}{19}$,EG=$\sqrt{A{E}^{2}-A{G}^{2}}$=$\frac{4\sqrt{57}}{19}$,
∴tan∠EAB=$\frac{EG}{AG}$=$\frac{\frac{4\sqrt{57}}{19}}{\frac{22\sqrt{19}}{19}}$=$\frac{2\sqrt{3}}{11}$.
故答案為:$\frac{2\sqrt{3}}{11}$.
點評 本題考查了全等三角形的判定與性質、等邊三角形的性質、勾股定理以及解直角三角形,利用勾股定理求出AG、EG的長度是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
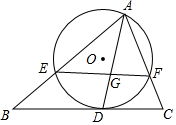 如圖,⊙O為△AEF的外接圓,BC與⊙O相切于點D,交AE,AF的延長線于點B,C.AD平分∠BAC,EF交AD于點G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.
如圖,⊙O為△AEF的外接圓,BC與⊙O相切于點D,交AE,AF的延長線于點B,C.AD平分∠BAC,EF交AD于點G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 環島是為了減少車輛行駛沖突,在多個交通路口交匯的地方設置的交通設施,多為圓形,它使車輛按統一方向行駛,將沖突點轉變為通行點,能有效地減少交通事故的發生,如圖是該交通環島的簡化模型(因路段FG施工,禁止從路段EF行駛過來的車輛在環島內通行,只能往環島外行駛),某時段內該交通環島的進出機動車輛數如圖所示,圖中箭頭方向表示車輛的行駛方向.
環島是為了減少車輛行駛沖突,在多個交通路口交匯的地方設置的交通設施,多為圓形,它使車輛按統一方向行駛,將沖突點轉變為通行點,能有效地減少交通事故的發生,如圖是該交通環島的簡化模型(因路段FG施工,禁止從路段EF行駛過來的車輛在環島內通行,只能往環島外行駛),某時段內該交通環島的進出機動車輛數如圖所示,圖中箭頭方向表示車輛的行駛方向.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,已知鈍角△ABC,依下列步驟尺規作圖,并保留作圖痕跡.
如圖,已知鈍角△ABC,依下列步驟尺規作圖,并保留作圖痕跡.| A. | BH垂直平分線段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | BC=CH |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com