
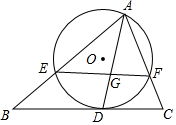
 如圖,⊙O為△AEF的外接圓,BC與⊙O相切于點D,交AE,AF的延長線于點B,C.AD平分∠BAC,EF交AD于點G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.
如圖,⊙O為△AEF的外接圓,BC與⊙O相切于點D,交AE,AF的延長線于點B,C.AD平分∠BAC,EF交AD于點G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值. 分析 連接DF,根據弦切角定理得到∠DAC=∠FDC,根據圓周角定理得到∠DAB=∠DFE,證明EF∥BC,根據相似三角形的性質計算即可.
解答 解: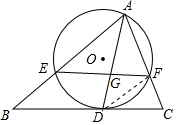 連接DF,
連接DF,
∵BC與⊙O相切,
∴∠DAC=∠FDC,
由圓周角定理得,∠DAB=∠DFE,
∵AD平分∠BAC,
∴∠DAC=∠DAB,
∴∠DFE=∠FDC,
∴EF∥BC,
∴$\frac{EG}{BD}$=$\frac{AG}{AD}$,$\frac{GF}{DC}$=$\frac{AG}{AD}$,
∴$\frac{EG}{BD}$=$\frac{GF}{DC}$,即$\frac{BD}{CD}$=$\frac{EG}{GF}$=$\frac{4}{3}$.
點評 本題考查的是相似三角形的判定和性質、切線的性質、圓周角定理的應用,掌握同弧或等弧所對的圓周角相等、相似三角形的判定定理和性質定理是解題的關鍵.


 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中數學 來源: 題型:解答題
| 價格 品種 地區 | 黃帝蕉 (元/千克) | 香牙蕉 (元/千克) |
| 海口 | 5 | 4.8 |
| 文昌 | 4.2 | 3.6 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在平面直角坐標系中,正方形ABCD的頂點A在y軸正半軸上,頂點B在x軸正半軸上,AC,OD交于點P,其中OA=4,OB=3.
如圖,在平面直角坐標系中,正方形ABCD的頂點A在y軸正半軸上,頂點B在x軸正半軸上,AC,OD交于點P,其中OA=4,OB=3.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
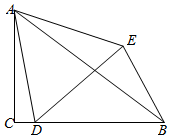 在Rt△ACB中,∠ACB=90°,點D在邊BC上,連接AD,以點D為頂點,AD為一邊作等邊△ADE,連接BE,若BC=7,BE=4,∠CBE=60°,則∠EAB的正切值為$\frac{2\sqrt{3}}{11}$.
在Rt△ACB中,∠ACB=90°,點D在邊BC上,連接AD,以點D為頂點,AD為一邊作等邊△ADE,連接BE,若BC=7,BE=4,∠CBE=60°,則∠EAB的正切值為$\frac{2\sqrt{3}}{11}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,一張長方形紙片的長AD=4,寬AB=1.點E在邊AD上,點F在BC邊上,將四邊形 ABFE沿直線EF翻折后,點B落在邊AD的中點G處,則EG等于( )
如圖,一張長方形紙片的長AD=4,寬AB=1.點E在邊AD上,點F在BC邊上,將四邊形 ABFE沿直線EF翻折后,點B落在邊AD的中點G處,則EG等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{17}{8}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com