
 如圖,一張長方形紙片的長AD=4,寬AB=1.點E在邊AD上,點F在BC邊上,將四邊形 ABFE沿直線EF翻折后,點B落在邊AD的中點G處,則EG等于( )
如圖,一張長方形紙片的長AD=4,寬AB=1.點E在邊AD上,點F在BC邊上,將四邊形 ABFE沿直線EF翻折后,點B落在邊AD的中點G處,則EG等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{17}{8}$ |
分析 作GM⊥BC于M,則GM=AB=1,DG=CM,由矩形的性質得出BC=AD=4,AD∥BC,由平行線的性質得出∠GEF=∠BFE,由折疊的性質得:GF=BF,∠GFE=∠BFE,得出∠GEF=∠GFE,證出EG=FG=BF,設EG=FG=BF=x,求出CM=DG=$\frac{1}{2}$AD=2,得出FM=BC-BF-CM=2-x,在Rt△GFM中,由勾股定理得出方程,解方程即可.
解答 解:作GM⊥BC于M,如圖所示: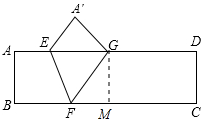
則GM=AB=1,DG=CM,
∵四邊形ABCD是矩形,
∴BC=AD=4,AD∥BC,
∴∠GEF=∠BFE,
由折疊的性質得:GF=BF,∠GFE=∠BFE,
∴∠GEF=∠GFE,
∴EG=FG=BF,
設EG=FG=BF=x,
∵G是AD的中點,∴CM=DG=$\frac{1}{2}$AD=2,
∴FM=BC-BF-CM=2-x,
在Rt△GFM中,由勾股定理得:FG2=FM2+GM2,
即x2=(2-x)2+12,
解得:x=$\frac{5}{4}$,即EG=$\frac{5}{4}$;
故選:C.
點評 本題考查了折疊的性質、矩形的性質、平行線的性質、勾股定理、等腰三角形的判定;熟練掌握折疊的性質,由勾股定理得出方程是解決問題的關鍵.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:解答題
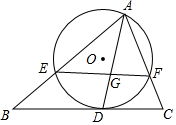 如圖,⊙O為△AEF的外接圓,BC與⊙O相切于點D,交AE,AF的延長線于點B,C.AD平分∠BAC,EF交AD于點G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.
如圖,⊙O為△AEF的外接圓,BC與⊙O相切于點D,交AE,AF的延長線于點B,C.AD平分∠BAC,EF交AD于點G,若$\frac{EG}{GF}$=$\frac{4}{3}$.求$\frac{BD}{CD}$的值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
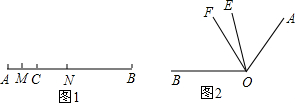
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,已知鈍角△ABC,依下列步驟尺規作圖,并保留作圖痕跡.
如圖,已知鈍角△ABC,依下列步驟尺規作圖,并保留作圖痕跡.| A. | BH垂直平分線段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | BC=CH |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 作圖:A,B兩村莊要建一個加油站,要求到A,B兩村距離相等,且到公路a,b的距離也相等,請你幫忙確定加油站的位置P.(用直尺、圓規作圖,保留作圖痕跡)
作圖:A,B兩村莊要建一個加油站,要求到A,B兩村距離相等,且到公路a,b的距離也相等,請你幫忙確定加油站的位置P.(用直尺、圓規作圖,保留作圖痕跡)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com