
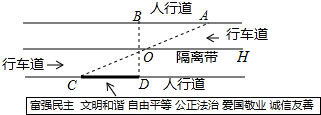
 楊陽同學沿一段筆直的人行道行走,在由A步行到達B處的過程中,通過隔離帶的空隙O,剛好瀏覽完對面人行道宣傳墻上的社會主義核心價值觀標語.其具體信息匯集如下,如圖,AB∥OH∥CD,相鄰兩平行線間的距離相等.AC,BD相交于O,OD⊥CD垂足為D.已知AB=20米.根據上述信息,標語CD的長度為20m.
楊陽同學沿一段筆直的人行道行走,在由A步行到達B處的過程中,通過隔離帶的空隙O,剛好瀏覽完對面人行道宣傳墻上的社會主義核心價值觀標語.其具體信息匯集如下,如圖,AB∥OH∥CD,相鄰兩平行線間的距離相等.AC,BD相交于O,OD⊥CD垂足為D.已知AB=20米.根據上述信息,標語CD的長度為20m. 分析 根據兩平行線間的距離相等得到OB=OD,再由一對直角相等,一對內錯角相等,利用ASA得到三角形AOB與三角形COD全等,利用全等三角形對應邊相等即可求出CD的長.
解答 解:∵AB∥OH∥CD,相鄰兩平行線間的距離相等,
∴OB=OD,
∵OB⊥AB,OD⊥DC,
∴∠ABO=∠CDO=90°,
在△ABO和△CDO中,
$\left\{\begin{array}{l}{∠ABO=∠CDO}\\{OB=OD}\\{∠AOB=∠COD}\end{array}\right.$,
∴△ABO≌△CDO(ASA),
∴CD=AB=20m,
故答案為:20
點評 此題考查了全等三角形的應用,垂直定義,以及平行線間的距離,熟練掌握全等三角形的判定與性質是解本題的關鍵.


科目:初中數學 來源: 題型:解答題
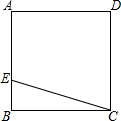 如圖,ABCD是一塊正方形場地,小華和小芳在AB邊上取定了一點E,測量知,EC=30m,EB=10m,這塊場地的面積和對角線長分別是多少?
如圖,ABCD是一塊正方形場地,小華和小芳在AB邊上取定了一點E,測量知,EC=30m,EB=10m,這塊場地的面積和對角線長分別是多少?查看答案和解析>>
科目:初中數學 來源: 題型:填空題
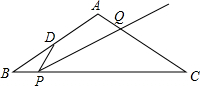 如圖,等腰△ABC中,AB=AC=4,BC=m,點D是邊AB的中點,點P是邊BC上的動點,且不與B、C重合,∠DPQ=∠B,射線PQ交AC于點Q.當點Q總在邊AC上時,m的最大值是4$\sqrt{2}$.
如圖,等腰△ABC中,AB=AC=4,BC=m,點D是邊AB的中點,點P是邊BC上的動點,且不與B、C重合,∠DPQ=∠B,射線PQ交AC于點Q.當點Q總在邊AC上時,m的最大值是4$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知,如圖,⊙O的半徑為6,弧$\widehat{AC}$的度數為120°,點B為弧$\widehat{AC}$的中點,點D為⊙O上異于A、B、C的三點,OE⊥AD于E,OF⊥CD于F,連接EF.
已知,如圖,⊙O的半徑為6,弧$\widehat{AC}$的度數為120°,點B為弧$\widehat{AC}$的中點,點D為⊙O上異于A、B、C的三點,OE⊥AD于E,OF⊥CD于F,連接EF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ±$\sqrt{6}$ | B. | 4 | C. | ±$\sqrt{6}$或4 | D. | 4或-$\sqrt{6}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,把長方形紙片ABCD沿EF折疊后,使得點D與點B重合,點C落在點C′的位置.
如圖,把長方形紙片ABCD沿EF折疊后,使得點D與點B重合,點C落在點C′的位置.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com