
分析 (1)如圖,作點A關于直線y=$\frac{1}{2}$x+1的對稱點C,連接BC交直線y=$\frac{1}{2}$x+1于M,此時|AM|+|BM|的值最小,最小值為BC的長.求出點C的坐標,再求出直線BC的解析式,解方程組可得點M坐標.
(2)利用三角形的面積公式計算即可.
解答 解:(1)如圖,作點A關于直線y=$\frac{1}{2}$x+1的對稱點C,連接BC交直線y=$\frac{1}{2}$x+1于M,此時|AM|+|BM|的值最小,最小值為BC的長.
∵直線AC的解析式為y=-2x,
由$\left\{\begin{array}{l}{y=-2x}\\{y=\frac{1}{2}x+1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{2}{5}}\\{y=\frac{4}{5}}\end{array}\right.$,
∴N(-$\frac{2}{5}$,$\frac{4}{5}$),
∵A(-1,2),AN=CN,B(-7,2)
∴C($\frac{1}{5}$,-$\frac{2}{5}$),
∴直線BC的解析式為y=-$\frac{1}{3}$x-$\frac{1}{3}$,
由$\left\{\begin{array}{l}{y=-\frac{1}{3}x-\frac{1}{3}}\\{y=\frac{1}{2}x+1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{8}{5}}\\{y=\frac{1}{5}}\end{array}\right.$,
∴點M坐標(-$\frac{8}{5}$,$\frac{1}{5}$),最小值為BC=$\sqrt{(-2-\frac{1}{5})^{2}+(7+\frac{2}{5})^{2}}$=$\frac{\sqrt{1490}}{5}$
(2)當|AM|+|BM|取得最小值時,△ABM的面積=$\frac{1}{2}$•6•(2-$\frac{1}{5}$)=$\frac{27}{5}$.
點評 本題考查軸對稱-最短問題、一次函數圖象上的點的特征,三角形的面積公式,兩點間距離公式等知識,解題的關鍵是學會求點關于直線的對稱點的坐標,屬于中考常考題型.


科目:初中數學 來源: 題型:填空題
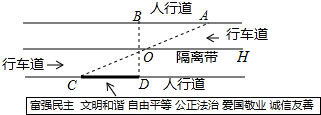 楊陽同學沿一段筆直的人行道行走,在由A步行到達B處的過程中,通過隔離帶的空隙O,剛好瀏覽完對面人行道宣傳墻上的社會主義核心價值觀標語.其具體信息匯集如下,如圖,AB∥OH∥CD,相鄰兩平行線間的距離相等.AC,BD相交于O,OD⊥CD垂足為D.已知AB=20米.根據上述信息,標語CD的長度為20m.
楊陽同學沿一段筆直的人行道行走,在由A步行到達B處的過程中,通過隔離帶的空隙O,剛好瀏覽完對面人行道宣傳墻上的社會主義核心價值觀標語.其具體信息匯集如下,如圖,AB∥OH∥CD,相鄰兩平行線間的距離相等.AC,BD相交于O,OD⊥CD垂足為D.已知AB=20米.根據上述信息,標語CD的長度為20m.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
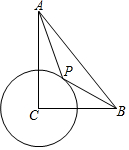 如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,則AP+$\frac{1}{2}$BP的最小值為( )
如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,則AP+$\frac{1}{2}$BP的最小值為( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2 $\sqrt{17}$ | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以點C為圓心,CA為半徑的圓與AB交于點D,則AD的長為$\frac{18}{5}$.
如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以點C為圓心,CA為半徑的圓與AB交于點D,則AD的長為$\frac{18}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
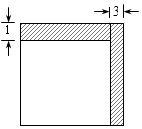 如圖,悅悅將一張正方形紙片剪去一個寬為3cm的長方形紙條,再從剩下的長方形紙片上剪去一個寬為1cm的長條,如果第一次剪下的長方形紙條的周長恰好是第二次剪下的長方形紙條周長的2倍.
如圖,悅悅將一張正方形紙片剪去一個寬為3cm的長方形紙條,再從剩下的長方形紙片上剪去一個寬為1cm的長條,如果第一次剪下的長方形紙條的周長恰好是第二次剪下的長方形紙條周長的2倍.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在如圖所示的2017年1月份的月歷表中,用一個3×2的長方形框圍住相鄰三列兩行中的6個數字,設其中第一行中間的數字為x.
在如圖所示的2017年1月份的月歷表中,用一個3×2的長方形框圍住相鄰三列兩行中的6個數字,設其中第一行中間的數字為x.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com