
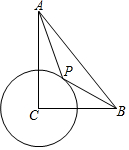
 如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動(dòng)點(diǎn),連結(jié)AP,BP,則AP+$\frac{1}{2}$BP的最小值為( )
如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動(dòng)點(diǎn),連結(jié)AP,BP,則AP+$\frac{1}{2}$BP的最小值為( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2 $\sqrt{17}$ | D. | 4 |
分析 連接CP,在CB上取點(diǎn)D,使CD=1,則有$\frac{CD}{CP}$=$\frac{CP}{CB}$=$\frac{1}{2}$,因?yàn)椤螾CD=∠BCP,所以△PCD∽△BCP,所以$\frac{PD}{BP}$=$\frac{1}{2}$,推出PD=$\frac{1}{2}$BP,所以AP+$\frac{1}{2}$BP=AP+PD,要使AP+$\frac{1}{2}$BP最小,只要AP+AD最小,當(dāng)點(diǎn)A,P,D在同一條直線時(shí),AP+AD最小,即:AP+$\frac{1}{2}$BP最小值為AD,求出AD即可
解答 解:如圖1,連接CP,在CB上取點(diǎn)D,使CD=1,則有$\frac{CD}{CP}$=$\frac{CP}{CB}$=$\frac{1}{2}$,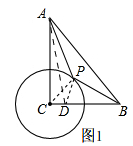
又∵∠PCD=∠BCP,
∴△PCD∽△BCP,
∴$\frac{PD}{BP}$=$\frac{1}{2}$,
∴PD=$\frac{1}{2}$BP,
∴AP+$\frac{1}{2}$BP=AP+PD.
要使AP+$\frac{1}{2}$BP最小,只要AP+AD最小,當(dāng)點(diǎn)A,P,D在同一條直線時(shí),AP+AD最小,
即:AP+$\frac{1}{2}$BP最小值為AD,
在Rt△ACD中,CD=1,AC=6,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{37}$,
AP+$\frac{1}{2}$BP的最小值為$\sqrt{37}$,
故選A.
點(diǎn)評 此題主要考查軸對稱-最短問題、勾股定理,相似三角形的判定和性質(zhì)、兩點(diǎn)之間線段最短等知識,解題的關(guān)鍵是學(xué)會(huì)添加輔助線,構(gòu)造相似三角形解決問題,屬于中考常考題型.


 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知,如圖,⊙O的半徑為6,弧$\widehat{AC}$的度數(shù)為120°,點(diǎn)B為弧$\widehat{AC}$的中點(diǎn),點(diǎn)D為⊙O上異于A、B、C的三點(diǎn),OE⊥AD于E,OF⊥CD于F,連接EF.
已知,如圖,⊙O的半徑為6,弧$\widehat{AC}$的度數(shù)為120°,點(diǎn)B為弧$\widehat{AC}$的中點(diǎn),點(diǎn)D為⊙O上異于A、B、C的三點(diǎn),OE⊥AD于E,OF⊥CD于F,連接EF.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,把長方形紙片ABCD沿EF折疊后,使得點(diǎn)D與點(diǎn)B重合,點(diǎn)C落在點(diǎn)C′的位置.
如圖,把長方形紙片ABCD沿EF折疊后,使得點(diǎn)D與點(diǎn)B重合,點(diǎn)C落在點(diǎn)C′的位置.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,一束光線從點(diǎn)O射出,照在經(jīng)過A(1,0)、B(0,1)的鏡面上的點(diǎn)D,經(jīng)AB反射后,反射光線又照到豎立在y軸位置的鏡面,經(jīng)y軸再反射的光線恰好通過點(diǎn)A,則點(diǎn)D的坐標(biāo)為($\frac{1}{3}$,$\frac{2}{3}$).
如圖,一束光線從點(diǎn)O射出,照在經(jīng)過A(1,0)、B(0,1)的鏡面上的點(diǎn)D,經(jīng)AB反射后,反射光線又照到豎立在y軸位置的鏡面,經(jīng)y軸再反射的光線恰好通過點(diǎn)A,則點(diǎn)D的坐標(biāo)為($\frac{1}{3}$,$\frac{2}{3}$).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com