
 如圖,一束光線從點O射出,照在經過A(1,0)、B(0,1)的鏡面上的點D,經AB反射后,反射光線又照到豎立在y軸位置的鏡面,經y軸再反射的光線恰好通過點A,則點D的坐標為($\frac{1}{3}$,$\frac{2}{3}$).
如圖,一束光線從點O射出,照在經過A(1,0)、B(0,1)的鏡面上的點D,經AB反射后,反射光線又照到豎立在y軸位置的鏡面,經y軸再反射的光線恰好通過點A,則點D的坐標為($\frac{1}{3}$,$\frac{2}{3}$). 分析 應先作出點O及點A的像,過兩個像的直線與直線AB的交點即為所求點.
解答 解:如圖所示,
∵點O關于AB的對稱點是O′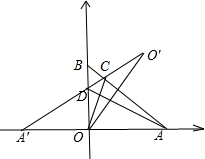 (1,1),
(1,1),
點A關于y軸的對稱點是A′(-1,0)
設AB的解析式為y=kx+b,
∵(1,0),(0,1)在直線上,
∴$\left\{\begin{array}{l}{k+b=0}\\{b=1}\end{array}\right.$,解得k=-1,
∴AB的表達式是y=1-x,
同理可得O′A′的表達式是y=$\frac{x}{2}$+$\frac{1}{2}$,
兩個表達式聯立,解得x=$\frac{1}{3}$,y=$\frac{2}{3}$.
故答案為:($\frac{1}{3}$,$\frac{2}{3}$).
點評 本題考查了軸對稱的知識;根據作相關點的像得到點D的位置是解決本題的關鍵.


科目:初中數學 來源: 題型:選擇題
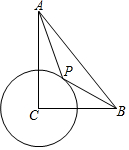 如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,則AP+$\frac{1}{2}$BP的最小值為( )
如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,則AP+$\frac{1}{2}$BP的最小值為( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2 $\sqrt{17}$ | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
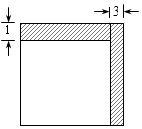 如圖,悅悅將一張正方形紙片剪去一個寬為3cm的長方形紙條,再從剩下的長方形紙片上剪去一個寬為1cm的長條,如果第一次剪下的長方形紙條的周長恰好是第二次剪下的長方形紙條周長的2倍.
如圖,悅悅將一張正方形紙片剪去一個寬為3cm的長方形紙條,再從剩下的長方形紙片上剪去一個寬為1cm的長條,如果第一次剪下的長方形紙條的周長恰好是第二次剪下的長方形紙條周長的2倍.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com