Question

5．已知△ABC分別以△ABC的AC，BC邊為腰，A，B為直角頂點，作等腰Rt△ACE和等腰Rt△BCD，M為ED的中點，求證：AM⊥BM．

Answer 1

分析 延長AM至F，使MF=AM，連接DF，BF，延長AC交DF于G．首先證明△DMF≌△EMA，推出∠MDF=∠MEA，DF∥AE，再證明△BDF≌△BCA，推出BF=BA，推出△BFA是等腰三角形，由此即可解決問題．

解答 證明：延長AM至F，使MF=AM，連接DF，BF，延長AC交DF于G 
∵M為ED中點，
∴MD=ME，
在△DMF和△EMA中，
$\left\{\begin{array}{l}{DM=EM}\\{∠DMF=∠EMA}\\{FM=AM}\end{array}\right.$，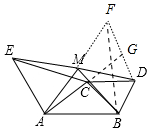
∴△DMF≌△EMA，
∴∠MDF=∠MEA，
∴DF∥AE，
∵△ACE，△BCD 都是等腰直角三角形，
∴∠GAE=90°，∠DBC=90°，
∵DF∥AE，
∴∠DGC=∠GAE=90°，
∵∠DBC=90°，
∴在四邊形DGCB中，∠BDF+∠BCG=360°-90°-90°=180°，
∵∠BCA+∠BCG=180°，
∴∠BDF=∠BCA，
∵△ACE，△BCD 都是等腰直角三角形，
∴BD=BC，AE=AC，
∵△DMF≌△EMA，
∴DF=AE，
∵AE=AC，
∴DF=AC，
在△BDF和△BCA中，
$\left\{\begin{array}{l}{DF=AC}\\{∠BDF=∠ACB}\\{BD=BC}\end{array}\right.$，
∴△BDF≌△BCA，
∴BF=BA，
∴△BFA是等腰三角形，
∵MF=AM，
∴BM⊥AF，
∴AM⊥BM．

點評 本題考查全等三角形的判定和性質、等腰直角三角形的性質、平行線的性質等知識，解題的關鍵是學會添加常用輔助線，構造全等三角形解決問題，屬于中考常考題型．