
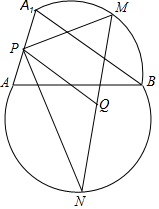
 AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉中心將弓形AMB順時針旋轉一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.
AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉中心將弓形AMB順時針旋轉一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.分析 設弦AB是⊙O的弦,連接NO,由此NO交AB于D,交⊙O于C,連接CA、CB、CM、BM,只要證明△PNM∽△ANC,即可推出∠MPN=90°,由此即可解決問題.
解答 證明:設弦AB是⊙O的弦,連接NO,由此NO交AB于D,交⊙O于C,連接CA、CB、CM、BM.
∵$\widehat{AN}$=$\widehat{BN}$,
∴OD⊥AB,
∴AD=BD,$\widehat{AC}$=$\widehat{BC}$,
∵$\widehat{{A}_{1}M}$=$\widehat{BM}$=$\widehat{BC}$,
∴BC=BM,
∵弓形AMB順時針旋轉一個角度成弓形A1MB,
∴AB=BA1,∠ABA1=∠CBM,
∴△BCM∽△BAA1,
∴∠MCB=∠A1AB,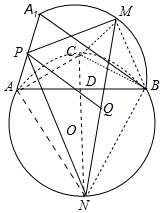 $\frac{CM}{A{A}_{1}}$=$\frac{BC}{BA}$,
$\frac{CM}{A{A}_{1}}$=$\frac{BC}{BA}$,
∵∠BAN=∠BCN,
∴∠PAN=∠MCN,
∵PA=PA1,
∴$\frac{CM}{A{A}_{1}}$=$\frac{CM}{2AP}$=$\frac{BC}{BA}$=$\frac{BC}{2BD}$,
∴$\frac{CM}{AP}$=$\frac{BC}{BD}$,
∵∠CDB=∠CAN=90°,∠CBD=∠ANC,
∴△DBC∽△ANC,
∴$\frac{BC}{BD}$=$\frac{NC}{NA}$,
∴$\frac{CM}{AP}$=$\frac{NC}{AN}$,
∴△APN∽△CMN,
∴$\frac{MN}{PN}$=$\frac{CN}{AN}$,∠CNM=∠PNA,
∴∠MNP=∠DNA,
∴△PNM∽△ANC,
∴∠NPM=∠NAC=90°,
∵MQ=QN,
∴PQ=QM=QN,
∴MN=2PQ.
點評 本題考查圓綜合題、相似三角形的判定和性質、垂徑定理等知識,解題的關鍵是學會添加常用輔助線,構造相似三角形解決問題,本題的難點多次證明相似三角形,熟練掌握兩邊成比例夾角相等兩三角形相似這個判定定理,屬于中考壓軸題.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | x2-(x-y+2z)=x2-x+y+2z | B. | 3x-[5x-(x-1)]=3x-5x-x+1 | ||
| C. | x-(-2x+3y-1)=x+2x-3y+1 | D. | (x-1)-(x2-2)=x-1-x2-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
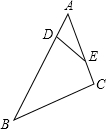 如圖,在△ABC中,點D、E分別在AB、AC邊上,且AD=2,AE=4,BD=10,CE=2,則DE:BC等于( )
如圖,在△ABC中,點D、E分別在AB、AC邊上,且AD=2,AE=4,BD=10,CE=2,則DE:BC等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
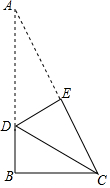 如圖,折疊直角三角形ABC紙片,使兩銳角頂點A、C重合,設折痕為DE.若AB=4,BC=3,則BD的值是( )
如圖,折疊直角三角形ABC紙片,使兩銳角頂點A、C重合,設折痕為DE.若AB=4,BC=3,則BD的值是( )| A. | $\frac{7}{8}$ | B. | 1 | C. | $\frac{9}{8}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com