
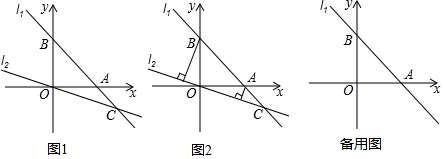
分析 (1)由點B的坐標是(0,6)、∠OAB=45°知OA=OB=6,即點A坐標為(6,0),根據(jù)點A、B坐標利用待定系數(shù)法可得一次函數(shù)l1的解析式,由一次函數(shù)l1和l2的解析式求得交點C的坐標,結合圖象可得答案;
(2)由∠AOB=90°知∠AOE+∠BOF=90°,再根據(jù)∠AEO=∠OFB=90°知∠AOE+∠OAE=90°,從而得∠BOF=∠OAE,結合OA=OB=6可證△AOE≌△OBF得AE=OF、OE=BF,即可知EF=OF+OE=AE+BF;
(3)分①k=1、②0<k<1、③k>1三種情況,與(2)同理證△AOE≌△OBF得AE=OF、OE=BF,結合圖形中EF轉(zhuǎn)化為線段的和或差即可得出答案.
解答 解:(1)∵點B的坐標是(0,6),∠OAB=45°,
∴OA=OB=6,即點A坐標為(6,0),
將點(6,0)、B(0,6)代入y1=ax+b得:
$\left\{\begin{array}{l}{6a+b=0}\\{b=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=6}\end{array}\right.$,
∴直線l1的解析式為:y=-x+6,
由$\left\{\begin{array}{l}{y=-x+6}\\{y=-\frac{1}{3}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{9}{2}}\\{y=-\frac{3}{2}}\end{array}\right.$,
由圖象可知當x<$\frac{9}{2}$時,直線l1位于直線l2上方,即y1>y2;
(2)EF=AE+BF,
如圖1,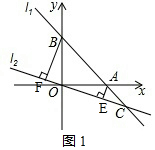
∵∠AOB=90°,
∴∠AOE+∠BOF=90°,
又∵∠AEO=∠OFB=90°,
∴∠AOE+∠OAE=90°,
∴∠BOF=∠OAE,
在△AOE和△OBF中,
∵$\left\{\begin{array}{l}{∠AEO=∠OFB}\\{∠OAE=∠BOF}\\{OA=BO}\end{array}\right.$,
∴△AOE≌△OBF(AAS),
∴AE=OF、OE=BF,
則EF=OF+OE=AE+BF;
(3)EF=|AE-BF|.
①如圖2,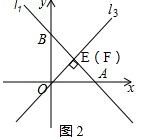
當l3:y=kx垂直于直線l1:y=-x+6時,即k=1,
由圖可知,點E與點F重合,
∵∠AOB=90°,∠OAB=45°,
∴∠OBA=45°,
∴AE=BF=OE,EF=0,
即EF=AE-BF;
②如圖3,當0<k<1時,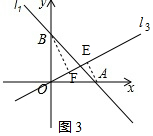
∵∠AOB=90°,
∴∠AOE+∠BOF=90°,
∵∠AEO=∠OFB=90°,
∴∠AOE+∠OAE=90°,
∴∠OAE=∠BOF,
在△AOE和△OBF中,
∵$\left\{\begin{array}{l}{∠OAE=∠BOF}\\{∠AEO=∠OFB}\\{OA=OB}\end{array}\right.$,
∴△AOE≌△OBF(AAS),
∴AE=OF、OE=BF,
則EF=OE-OF=BF-AE;
③如圖4,當k>1時,
與②同理可得△AOE≌△OBF,
∴AE=OF、OE=BF,
則EF=OF-OE=BF-AE;
綜上,EF=|AE-BF|.
點評 本題主要考查一次函數(shù)的綜合、全等三角形的判定與性質(zhì)等知識點,熟練掌握待定系數(shù)法求函數(shù)的解析式及兩直線相交的問題是解題的根本,構建全等三角形將分散的線段轉(zhuǎn)移到同一條直線上是解題的關鍵.


科目:初中數(shù)學 來源: 題型:填空題
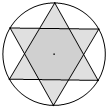 如圖所示的“六芒星”圖標是由圓的六等分點連接而成,若圓的半徑為2$\sqrt{3}$,則圖中陰影部分的面積為12$\sqrt{3}$.
如圖所示的“六芒星”圖標是由圓的六等分點連接而成,若圓的半徑為2$\sqrt{3}$,則圖中陰影部分的面積為12$\sqrt{3}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| 全球通 | 神州行 | |
| 月租費 | 30元/月 | 0 |
| 本地通話費 | 0.10元/分鐘 | 0.30元/分鐘 |
| 全球通(元) | 神州行(元) | |
| 100分 | 30+100×0.10=40元 | 100×0.30=30元 |
| 200分 | 30+200×0.10=50元 | 200×0.30=60元 |
| x分鐘 | (30+0.1x)元 | 0.3x元 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
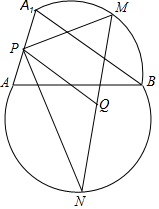 AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉(zhuǎn)中心將弓形AMB順時針旋轉(zhuǎn)一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.
AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉(zhuǎn)中心將弓形AMB順時針旋轉(zhuǎn)一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | a=1 | B. | a=-2 或a=1 | C. | a=-5 | D. | a=-2或a=-5 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com