
分析 由于a、b、c都是正數,根據不等式的性質,去掉分式的分母,整理不等式,根據完全平方公式和非負數的性質,得到a、b、c間關系,把a、b、c間關系代入代數式2c2-ac-bc-4c+2,變形成(c-m)2±n的形式,確定最小值.
解答 解:∵$\frac{a}{bc}$+$\frac{b}{ca}$+$\frac{c}{ab}$≤$\frac{2}{a}$+$\frac{2}{b}$-$\frac{2}{c}$,
∴$\frac{{a}^{2}}{abc}$+$\frac{{b}^{2}}{abc}$+$\frac{{c}^{2}}{abc}$≤$\frac{2bc}{abc}$+$\frac{2ac}{abc}$-$\frac{2ab}{abc}$,
∵a,b,c都是正數,
∴a2+b2+c2≤2bc+2ac-2ab,
即a2+b2+c2-2bc-2ac+2ab≤0
(a+b)2-2c(a+b)+c2≤0
∴(a+b-c)2≤0
∴a+b=c.
∵2c2-ac-bc-4c+2
=2c2-c(a+b)-4c+2
由于a+b=c,
∴2c2-c(a+b)-4c+2
=c2-4c+2
=(c-2)2-2
∵(c-2)2≥0
∴(c-2)2-2的最小值是-2.
點評 本題考查了完全平方公式、不等式的性質、非負數的性質、配方法及分式的化簡求值.解決本題有兩個關鍵:(1)根據完全平方公式和非負數的性質確定a、b、c間關系;(2)把要求最小值的代數式變形成(c-m)2±n的形式.


科目:初中數學 來源: 題型:選擇題
| A. | -$\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 0 | D. | -2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 全球通 | 神州行 | |
| 月租費 | 30元/月 | 0 |
| 本地通話費 | 0.10元/分鐘 | 0.30元/分鐘 |
| 全球通(元) | 神州行(元) | |
| 100分 | 30+100×0.10=40元 | 100×0.30=30元 |
| 200分 | 30+200×0.10=50元 | 200×0.30=60元 |
| x分鐘 | (30+0.1x)元 | 0.3x元 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
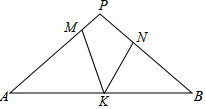 如圖,在△PAB中,PA=PB,M,N,K分別是PA,PB,AB上的點,且AM=BK,BN=AK,若∠MKN=44°,則∠P的度數為92°.
如圖,在△PAB中,PA=PB,M,N,K分別是PA,PB,AB上的點,且AM=BK,BN=AK,若∠MKN=44°,則∠P的度數為92°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
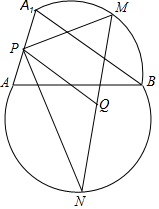 AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉中心將弓形AMB順時針旋轉一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.
AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉中心將弓形AMB順時針旋轉一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com