
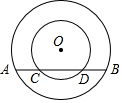
 如圖,兩個同心圓,大圓半徑為10cm,小圓的半徑為6cm,若大圓的弦AB與小圓相交,則弦AB的取值范圍是16<AB≤20.
如圖,兩個同心圓,大圓半徑為10cm,小圓的半徑為6cm,若大圓的弦AB與小圓相交,則弦AB的取值范圍是16<AB≤20. 分析 解決此題首先要弄清楚AB在什么時候最大,什么時候最小.當AB與小圓相切時有一個公共點,此時可知AB最小;當AB經過同心圓的圓心時,弦AB最大且與小圓相交有兩個公共點,此時AB最大,由此可以確定所以AB的取值范圍.
解答 解:如圖所示,
當AB與小圓相切時有一個公共點D,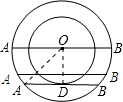
連接OA,OD,可得OD⊥AB,
∴D為AB的中點,即AD=BD,
在Rt△ADO中,OD=6,OA=10,
∴AD=8,
∴AB=2AD=16;
當AB經過同心圓的圓心時,弦AB最大且與小圓相交有兩個公共點,
此時AB=20,
所以AB的取值范圍是16<AB≤20.
故答案為:16<AB≤20.
點評 此題考查了直線與圓的位置關系,涉及的知識有:垂徑定理,勾股定理,以及切線的性質,其中解題的關鍵是抓住兩個關鍵點:1、當弦AB與小圓相切時最短;2、當AB過圓心O時最長.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:選擇題
| A. | (k2+1)x2-4=0 | B. | ax2+bx+c=0 | C. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-3=0 | D. | (x+4)(x-2)=x2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 全球通 | 神州行 | |
| 月租費 | 30元/月 | 0 |
| 本地通話費 | 0.10元/分鐘 | 0.30元/分鐘 |
| 全球通(元) | 神州行(元) | |
| 100分 | 30+100×0.10=40元 | 100×0.30=30元 |
| 200分 | 30+200×0.10=50元 | 200×0.30=60元 |
| x分鐘 | (30+0.1x)元 | 0.3x元 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
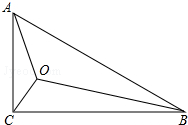 在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,點O為Rt△ABC內一點,連接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,則OA+OB+OC=$\sqrt{7}$.
在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,點O為Rt△ABC內一點,連接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,則OA+OB+OC=$\sqrt{7}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
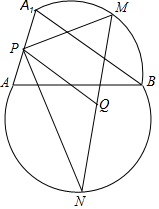 AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉中心將弓形AMB順時針旋轉一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.
AB是圓的一條弦,它將圓分成兩部分,M、N分別是兩段弧的中點,以點B旋轉中心將弓形AMB順時針旋轉一個角度成弓形A1MB、A1A的中點為P,MN的中點為Q.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com