
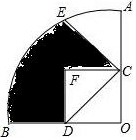
 如圖,在圓心角為90°的扇形AOB中,半徑OA=2,點C、D分別是OA、OB的中點,點E是$\widehat{AB}$的一個三等分點,將△COD沿CD折疊,點O落在點F處,則圖中陰影部分的面積為$\frac{2}{3}$π-$\frac{1}{2}$.
如圖,在圓心角為90°的扇形AOB中,半徑OA=2,點C、D分別是OA、OB的中點,點E是$\widehat{AB}$的一個三等分點,將△COD沿CD折疊,點O落在點F處,則圖中陰影部分的面積為$\frac{2}{3}$π-$\frac{1}{2}$. 分析 先證明△BOE是等邊三角形,再證明ED∥AO得S△CDE=S△EDO所以S陰=S扇形OBE-S△CDF此即可計算.
解答 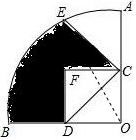 解:∵E為弧AB的一個三等分點,∠AOB=90°,
解:∵E為弧AB的一個三等分點,∠AOB=90°,
∴∠AOE=30°,∠BOE=60°,
∵OB=OE,
∴△BOE是等邊三角形,
∵BD=DO,
∴ED⊥BO,
∵BO⊥AO,
∴ED∥AO,
∴S△CDE=S△EDO,
∴S陰=S扇形OBE-S△CDF=$\frac{60π•{2}^{2}}{360}$-$\frac{1}{2}×$1×1=$\frac{2}{3}$π-$\frac{1}{2}$.
故答案為:$\frac{2}{3}$π-$\frac{1}{2}$.
點評 本題考查扇形的面積、等邊三角形的判定和性質(zhì)、同底等高的三角形面積相等,解題的關(guān)鍵是把不規(guī)則圖形轉(zhuǎn)化為規(guī)則圖形進(jìn)行計算,屬于中考常考題型.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 正多邊形的外接圓的圓心,就是它的中心 | |
| B. | 正多邊形的外接圓的半徑,就是它的半徑 | |
| C. | 正多邊形的內(nèi)切圓的半徑,就是它的邊心距 | |
| D. | 正多邊形的外接圓的圓心角,就是它的中心角 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
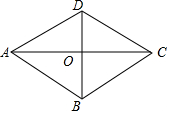 已知?ABCD的對角線AC,BD相交于點O,AD=$\sqrt{13}$,AC=6,BD=4,你認(rèn)為四邊形ABCD是菱形嗎?請說明理由.
已知?ABCD的對角線AC,BD相交于點O,AD=$\sqrt{13}$,AC=6,BD=4,你認(rèn)為四邊形ABCD是菱形嗎?請說明理由.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 110° | B. | 35° | C. | 140° | D. | 55° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com