

分析 模型建立:根據折疊的性質即可得出BC=BE,BE=AE,代換即可得出結論;
模型應用:(1)先根據模型建立中的結論依次求出OB,OE,最后用勾股定理即可求出BE,即可得出結論.
(2)求是否會受到臺風的影響,其實就是求A到BC的距離是否大于臺風影響范圍的半徑,如果大于,則不受影響,反之則受影響.如果過A作AD⊥BC于D,AD就是所求的線段.直角三角形ABD中,有∠ABD的度數,有AB的長,AD就不難求出了.然后根據題目給出的條件判斷出時幾級風.
解答 解:模型建立:BC與AB的關系為AB=2BC,
【】里面是折疊出∠A=30°的理由,
【由折疊得,∠CBD=∠ABD=∠A,
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠CBD+∠ABD+∠A=90°,
∴∠A=30°,】
理由:由折疊得,BC=BE,BE=AE,
∴AB=AE+BE=2BE=2BC,
模型應用:(1)如圖2,根據模型建立的結論,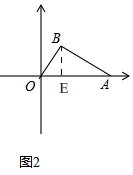 在Rt△OAB中,∠OAB=30°,OA=4,
在Rt△OAB中,∠OAB=30°,OA=4,
∴∠AOB=90°-∠OAB=60°,OB=$\frac{1}{2}$OA=2,
過點B作BE⊥OA于E,
∴∠AEB=90°,
∴∠OBE=90°-∠AOB=30°,
∴OE=$\frac{1}{2}$OB=1,
在Rt△OBE中,根據勾股定理得,BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=$\sqrt{3}$,
∴B(1,$\sqrt{3}$);
(2)該城市會受到這次臺風的影響.
理由是:如圖3,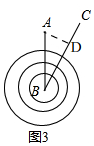 過A作AD⊥BC于D.在Rt△ABD中,
過A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=200,
∴AD=$\frac{1}{2}$AB=100,
∵城市受到的風力達到或超過四級,則稱受臺風影響,
∴受臺風影響范圍的半徑為20×(12-4)=160.
∵100<160,
∴該城市會受到這次臺風的影響;
∴該城市受到這次臺風最大風力為:12-(100÷20)=7(級).
點評 此題是幾何變換綜合題,主要考查了折疊的性質,勾股定理的應用,解本題的關鍵是由折疊得出含30°的直角三角形性質,將實際問題轉化為直角三角形中的數學問題,可通過作輔助線構造直角三角形,再把條件和問題轉化到直角三角形中,使問題解決.


科目:初中數學 來源: 題型:填空題
 如圖所示,長方形OABC的頂點A在x軸上,C在y軸上,點B坐標為(4,2),若直線y=mx-1恰好將長方形分成面積相等的兩部分,則m的值為1.
如圖所示,長方形OABC的頂點A在x軸上,C在y軸上,點B坐標為(4,2),若直線y=mx-1恰好將長方形分成面積相等的兩部分,則m的值為1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
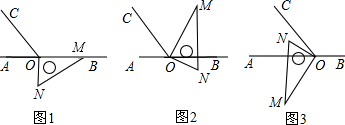
 如圖,AC分別切⊙O于D、E,作OQ⊥BC交⊙O于P,連DP、EP交BC于G、F,AF、AG分別交DG、EF于M、N.求證:OQ⊥MN.
如圖,AC分別切⊙O于D、E,作OQ⊥BC交⊙O于P,連DP、EP交BC于G、F,AF、AG分別交DG、EF于M、N.求證:OQ⊥MN.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
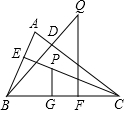 已知:如圖,在銳角△ABC中,BD,CE分別是△ABC的AC,AB邊上的高,在CE上截取CP=AB,過點P作PG⊥BC于G點,在BD的延長線上截取BQ=AC,過點Q作QF⊥BC于F點,求證:PG+QF=BC.
已知:如圖,在銳角△ABC中,BD,CE分別是△ABC的AC,AB邊上的高,在CE上截取CP=AB,過點P作PG⊥BC于G點,在BD的延長線上截取BQ=AC,過點Q作QF⊥BC于F點,求證:PG+QF=BC.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com