
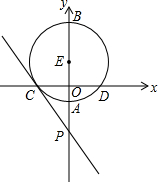
 如圖,在平面直角坐標系中,以E(0,1)為圓心,3為半徑的⊙E交y軸于A、B兩點,交x軸于C、D兩點,點P的坐標為(0,-8)
如圖,在平面直角坐標系中,以E(0,1)為圓心,3為半徑的⊙E交y軸于A、B兩點,交x軸于C、D兩點,點P的坐標為(0,-8)分析 (1)連接CE,分別求出OC,OA,OB的長,即可求出點C,點A,點B的坐標;
(2)利用勾股定理的逆定理證明∠ECP=90°即可證明PC是⊙E的切線.
解答 解:
(1)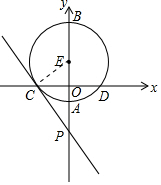 連接CE,
連接CE,
∵圓E的半徑為3,(0,1)為圓心,
∴OE=1,OA=2,CE=3,
∴OC=$\sqrt{C{E}^{2}-O{E}^{2}}$=2$\sqrt{2}$,
∵OE⊥CD,
∴OD=CD=2$\sqrt{2}$,
∴AB=6,
∴OB=6-2=4,
∴點A,B,C三點的坐標分別為:(0,-2);(0,4);(-2$\sqrt{2}$,0),
故答案為:(0,-2);(0,4);(-2$\sqrt{2}$,0);
(2)證明:
∵點P的坐標為(0,-8),
∴OP=8,
∵OC=2$\sqrt{2}$,
∴PC=$\sqrt{O{C}^{2}+O{P}^{2}}$=6$\sqrt{2}$,
∵PE=9,CE=3,
∴PC2+CE2=PE2,
∴△ECP是直角三角形,
∴∠ECP=90°,
∴CE⊥PC,
∴PC是⊙E的切線.
點評 本題主要考查了切線的判定定理運用、垂徑定理的運用以及勾股定理以及其逆定理的運用,熟練掌握和圓有關的各種性質是解題的關鍵.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
 在數學活動課上,老師帶領學生去測量操場上樹立的旗桿的高度,老師為同學們準備了如下工具:①高為m米的測角儀,②長為n米的竹竿,③足夠長的皮尺.請你選用以上的工具,設計一個可以通過測量,求出國旗桿高度的方案(不用計算和說明,畫出圖形并標記可以測量的長度或者角度即可,可測量的角度選用α,β,γ標記,可測量的長度選用a,b,c,d標記,測角儀和竹竿可以用線段表示).
在數學活動課上,老師帶領學生去測量操場上樹立的旗桿的高度,老師為同學們準備了如下工具:①高為m米的測角儀,②長為n米的竹竿,③足夠長的皮尺.請你選用以上的工具,設計一個可以通過測量,求出國旗桿高度的方案(不用計算和說明,畫出圖形并標記可以測量的長度或者角度即可,可測量的角度選用α,β,γ標記,可測量的長度選用a,b,c,d標記,測角儀和竹竿可以用線段表示).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
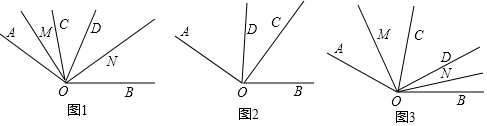
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
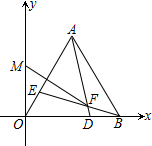 如圖,在平面直角坐標系中,等邊△OAB的邊OB在x軸正半軸上,點A(3,m),m>0,點D、E分別從B、O以相同的速度向O、A運動,連接AD、BE,交點為F,M是y軸上一點,則FM的最小值是( )
如圖,在平面直角坐標系中,等邊△OAB的邊OB在x軸正半軸上,點A(3,m),m>0,點D、E分別從B、O以相同的速度向O、A運動,連接AD、BE,交點為F,M是y軸上一點,則FM的最小值是( )| A. | 3 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com