
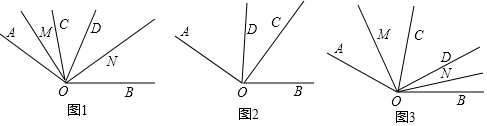
分析 (1)①根據角平分線的定義,得出∠AOM=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD,再根據∠AOB=α,∠COD=180°-α,得出∠AOC+∠BOD=∠AOB-∠COD=α-(180°-α)=2α-180°,進而得出∠AOM+∠BON=$\frac{1}{2}$(2α-180°)=α-90°,最后根據∠MON=∠AOB-(∠AOM+∠BON)進行計算即可;②根據①中的方法進行計算,即可得出∠MON的度數;
(2)先根據角平分線的定義,得出∠AOM=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD,再根據∠AOB=α,∠COD=kα,得出∠AOC+∠BOD=∠AOB-∠COD=α-kα,進而得到∠AOM+∠BON=$\frac{1}{2}$(α-kα)=$\frac{1}{2}$α(1-k),最后根據∠MON=∠AOB-(∠AOM+∠BON)進行計算即可.
解答  解:(1)①如圖1,∵OM平分∠AOC,ON平分∠BOD,
解:(1)①如圖1,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD,
∴∠AOM+∠BON=$\frac{1}{2}$(∠AOC+∠BOD),
∵∠AOB=α,∠COD=180°-α,
∴∠AOC+∠BOD=∠AOB-∠COD=α-(180°-α)=2α-180°,
∴∠AOM+∠BON=$\frac{1}{2}$(2α-180°)=α-90°,
∴∠MON=∠AOB-(∠AOM+∠BON)=α-(α-90°)=90°;
②當OC在OD右側,補全圖形如圖2所畫,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD,
∵∠AOB=α,∠COD=180°-α,
∴∠AOC+∠BOD=∠AOB+∠COD=α+(180°-α)=180°,
∴∠AOM+∠BON=$\frac{1}{2}$×180°=90°,
∴∠MON=∠AOB-(∠AOM+∠BON)=α-90°;
(2)∠MON的度數為$\frac{1}{2}$(1+k)α.
理由:如圖3,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=$\frac{1}{2}$∠AOC,∠BON=$\frac{1}{2}$∠BOD,
∴∠AOM+∠BON=$\frac{1}{2}$(∠AOC+∠BOD),
∵∠AOB=α,∠COD=kα,
∴∠AOC+∠BOD=∠AOB-∠COD=α-kα,
∴∠AOM+∠BON=$\frac{1}{2}$(α-kα)=$\frac{1}{2}$α(1-k),
∴∠MON=∠AOB-(∠AOM+∠BON)=α-$\frac{1}{2}$α(1-k)=$\frac{1}{2}$(1+k)α.
點評 本題主要考查了角的計算以及角平分線的定義的運用,解決問題的關鍵是運用角的和差關系進行計算.解題時注意:從一個角的頂點出發,把這個角分成相等的兩個角的射線叫做這個角的平分線.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:填空題
 如圖,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是$\frac{15\sqrt{3}}{4}$-$\frac{3}{2}$π.
如圖,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是$\frac{15\sqrt{3}}{4}$-$\frac{3}{2}$π.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
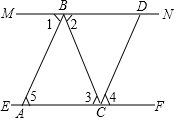 如圖,MN、EF是兩面互相平行的鏡面,光線AB照射到鏡面MN上,反射光線為BC,光線BC又經鏡面EF反射后,反射光線為CD,已知入射光線與反射光線和鏡面所成的角相等(即∠1=∠2,∠3=∠4),試說明AB∥CD,根據下列解答填空(理由或數學式).
如圖,MN、EF是兩面互相平行的鏡面,光線AB照射到鏡面MN上,反射光線為BC,光線BC又經鏡面EF反射后,反射光線為CD,已知入射光線與反射光線和鏡面所成的角相等(即∠1=∠2,∠3=∠4),試說明AB∥CD,根據下列解答填空(理由或數學式).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
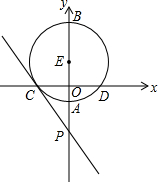 如圖,在平面直角坐標系中,以E(0,1)為圓心,3為半徑的⊙E交y軸于A、B兩點,交x軸于C、D兩點,點P的坐標為(0,-8)
如圖,在平面直角坐標系中,以E(0,1)為圓心,3為半徑的⊙E交y軸于A、B兩點,交x軸于C、D兩點,點P的坐標為(0,-8)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
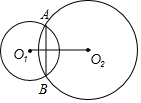 如圖,⊙O1與⊙O2相交于A、B兩點,⊙O1與⊙O2的半徑分別是1和$\sqrt{3}$,O1O2=2,那么兩圓公共弦AB的長為$\sqrt{3}$.
如圖,⊙O1與⊙O2相交于A、B兩點,⊙O1與⊙O2的半徑分別是1和$\sqrt{3}$,O1O2=2,那么兩圓公共弦AB的長為$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com