
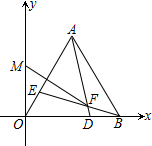
 如圖,在平面直角坐標系中,等邊△OAB的邊OB在x軸正半軸上,點A(3,m),m>0,點D、E分別從B、O以相同的速度向O、A運動,連接AD、BE,交點為F,M是y軸上一點,則FM的最小值是( )
如圖,在平面直角坐標系中,等邊△OAB的邊OB在x軸正半軸上,點A(3,m),m>0,點D、E分別從B、O以相同的速度向O、A運動,連接AD、BE,交點為F,M是y軸上一點,則FM的最小值是( )| A. | 3 | B. | $\sqrt{3}$+1 | C. | 2$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
分析 先判斷出△OBE≌△DAB(SAS),即可判斷出∠AFB=120°,即可判斷出點F是以O'為圓心的圓上的一段弧(劣弧$\widehat{AB}$),然后確定出圓心O'的位置及坐標,設出點M的坐標,即可確定當點M(0,2$\sqrt{3}$)時,FM的最小值是6-2$\sqrt{3}$.
解答 解:如圖, ∵△OAB是等邊三角形,
∵△OAB是等邊三角形,
∴∠AOB=∠ABD=60°,OB=AB,
∵點D、E分別從B、O以相同的速度向O、A運動,
∴BD=OE,在△OBE和△DAB中,$\left\{\begin{array}{l}{OE=BD}\\{∠BOE=∠ABD=60°}\\{OB=AB}\end{array}\right.$,
∴△OBE≌△DAB(SAS),
∴∠OBE=∠BAD,
∴∠ABE+∠BAD=∠ABE+∠OBE=∠ABO=60°
∴∠AFB=180°-(∠ABE+∠BAD)=120°,
∴點F是經過點A,B,F的圓上的點,記圓心為O',在⊙O'上取一點N,使點N和點F在弦AB的兩側,連接AN,BN,
∴∠ANB=180°-∠AFB=60°,
連接O'A,O'B,
∴∠AO'B=2∠ANB=120°,
∵O'A=O'B,
∴∠ABO'=∠BAO',
∴∠ABO'=$\frac{1}{2}$(180°-∠AO'B)=$\frac{1}{2}$(180°-120°)=30°,
∵∠ABO=60°,
∴∠OBO'=90°,
∵△AOB是等邊三角形,A(3,m),
∴AB=OB=2×3,m=3$\sqrt{3}$,
過點O'作O'G⊥AB,
∴BG=$\frac{1}{2}$AB=3,
在Rt△BO'G中,∠ABO'=30°,BG=3,
∴O'B=$\frac{BG}{cos∠ABO'}$=$\frac{3}{cos30°}$=2$\sqrt{3}$,
∴O'(6,2$\sqrt{3}$),
設M(0,n),
∴O'M=$\sqrt{36+(n-2\sqrt{3})^{2}}$
∴FM=O'M-O'F=$\sqrt{36+(n-2\sqrt{3})^{2}}$-2$\sqrt{3}$,
只有n-2$\sqrt{3}$=0時,(n-2$\sqrt{3}$)2最小為0,即$\sqrt{36+(n-2\sqrt{3})^{2}}$最小為6.
當n-2$\sqrt{3}$=0時,即:n=2$\sqrt{3}$時,FM最小,
∴FM的最小值=6-2$\sqrt{3}$.
故選D.
點評 此題是圓的綜合題,主要考查了等邊三角形的性質,全等三角形的性質和判定,勾股定理等知識點;找出點F的運動軌跡是解本題的關鍵也是難點,是一道很好的定弦定角最值問題.解此類題目的方法是判斷出動點的軌跡所在的圓的圓心和確定出半徑.


 小題狂做系列答案
小題狂做系列答案科目:初中數學 來源: 題型:解答題
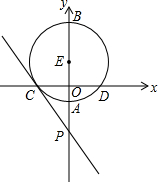 如圖,在平面直角坐標系中,以E(0,1)為圓心,3為半徑的⊙E交y軸于A、B兩點,交x軸于C、D兩點,點P的坐標為(0,-8)
如圖,在平面直角坐標系中,以E(0,1)為圓心,3為半徑的⊙E交y軸于A、B兩點,交x軸于C、D兩點,點P的坐標為(0,-8)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
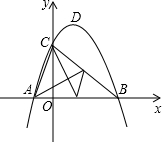 如圖,已知拋物線y=ax2+bx+3與x軸交于A,B兩點(A,B分別在原點的左右兩側),與y軸交于點C,拋物線的頂點為點D,且OA:OB:OC=1:3:3,求拋物線的解析式及頂點D的坐標.
如圖,已知拋物線y=ax2+bx+3與x軸交于A,B兩點(A,B分別在原點的左右兩側),與y軸交于點C,拋物線的頂點為點D,且OA:OB:OC=1:3:3,求拋物線的解析式及頂點D的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 里程(千米) | 0<x≤3 | 3<x≤6 | x>6 |
| 價格 | N元 | $\frac{22}{N}$元/千米 | $\frac{25}{N}$元/千米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com