

分析 (1)根據運動速度和時間分別求得CM、BD的長,根據線段的和差計算可得;
(2)由題意得CM=2 cm、BD=4 cm,根據AC+MD=AM-CM+BM-BD=AB-CM-BD可得答案;
(3)根據C、D的運動速度知BD=2MC,再由已知條件MD=2AC求得MB=2AM,所以AM=$\frac{1}{3}$AB;
(4)分點N在線段AB上時和點N在線段AB的延長線上時分別求解可得.
解答 解:(1)根據題意知,CM=2cm,BD=4cm,
∵AB=12cm,AM=4cm,
∴BM=8cm,
∴AC=AM-CM=2cm,DM=BM-BD=4cm,
故答案為:2,4;
(2)當點C、D運動了2 s時,CM=2 cm,BD=4 cm
∵AB=12 cm,CM=2 cm,BD=4 cm
∴AC+MD=AM-CM+BM-BD=AB-CM-BD=12-2-4=6 cm;
(3)根據C、D的運動速度知:BD=2MC,
∵MD=2AC,
∴BD+MD=2(MC+AC),即MB=2AM,
∵AM+BM=AB,
∴AM+2AM=AB,
∴AM=$\frac{1}{3}$AB=4,
故答案為:4;
(4)①當點N在線段AB上時,如圖1,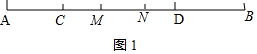
∵AN-BN=MN,
又∵AN-AM=MN
∴BN=AM=4
∴MN=AB-AM-BN=12-4-4=4
∴$\frac{MN}{AB}$=$\frac{4}{12}$=$\frac{1}{3}$;
②當點N在線段AB的延長線上時,如圖2,
∵AN-BN=MN,
又∵AN-BN=AB
∴MN=AB=12
∴$\frac{MN}{AB}$=$\frac{12}{12}$=1;
綜上所述$\frac{MN}{AB}$=$\frac{1}{3}$或1.
點評 本題考查了兩點間的距離,靈活運用線段的和、差、倍、分轉化線段之間的數量關系是十分關鍵的一點.


 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
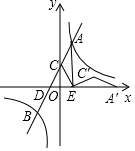 已知一次函數y1=k1x+b與反比例函數y2=$\frac{{k}_{2}}{x}$相交于點A、B,與y軸交于點C,與x軸交于點D,過點A作AE⊥x軸于點E,點O為DE中點,連接CE,已知S△ADE=4,tan∠DCO=$\frac{1}{2}$.
已知一次函數y1=k1x+b與反比例函數y2=$\frac{{k}_{2}}{x}$相交于點A、B,與y軸交于點C,與x軸交于點D,過點A作AE⊥x軸于點E,點O為DE中點,連接CE,已知S△ADE=4,tan∠DCO=$\frac{1}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠C=90°,∠B=30°,以點A為圓心,任意長為半徑畫弧分別交AB,AC于點M和N,再分別以點M,N為圓心畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )
如圖,在△ABC中,∠C=90°,∠B=30°,以點A為圓心,任意長為半徑畫弧分別交AB,AC于點M和N,再分別以點M,N為圓心畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,平行四邊形ABCD的兩條對角線相交于O,且AC平分∠DAB.
如圖,平行四邊形ABCD的兩條對角線相交于O,且AC平分∠DAB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com