
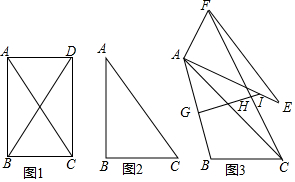
分析 (1)①當n=90°時,圖象如圖所示.②如圖1中,作HM⊥BF于M.設CB=AD=AF=a,AB=b,首先證明MG=MH=$\frac{1}{2}$a,推出∠AGI=45°即可證明.
(2)結論仍然成立.如圖2中,連接FB、DF,作FN⊥BC于N,交AD于K,作HM⊥AB于M,交BF于O,交FN于Q,作GP⊥FN于P,連接OG、OP,作OJ⊥GP于J.
首先證明△FKD∽△PQH,推出∠FDK=∠QHP,再證明∠QHP=∠AGH,推出∠AIG=∠AFD=∠AGI,即可解決問題.
解答 (1)①解:當n=90°時,圖象如圖所示.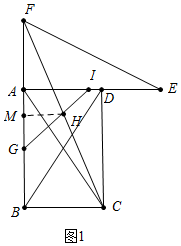
②證明:如圖1中,作HM⊥BF于M.設CB=AD=AF=a,AB=b,
∵FH=HC,HM∥BC,
∴FM=BM=$\frac{a+b}{2}$,
∴HM=$\frac{1}{2}$a,
∵BG=$\frac{1}{2}$AB=$\frac{1}{2}$b,
∴MG=BM-GB=$\frac{1}{2}$(a+b)-$\frac{1}{2}$b=$\frac{1}{2}$a,
∴MG=MH,
∴∠MGH=∠MHG=45°,
∵∠GAI=90°,
∴∠AGI=∠AIG=45°,
∴AG=AI,
∵AB=AE,AG=GB,
∴AI=IE.
(2)解:結論仍然成立.理由如下,
如圖2中,連接FB、DF,作FN⊥BC于N,交AD于K,作HM⊥AB于M,交BF于O,交FN于Q,作GP⊥FN于P,連接OG、OP,作OJ⊥GP于J.
∵HM∥BC,FH=HC,
∴FQ=QN,FO=OB,
∵AG=BG,
∴AF=2OG,BN=2OQ=2OM,CN=DK=2QI,PK=PN,設AB=m,PQ=n,
∵FQ=QN=$\frac{m}{2}$+n,KQ=$\frac{m}{2}$-n,FK=FQ-KQ=$\frac{m}{2}$+n-($\frac{m}{2}-n$)=2n,
∴FK=2PQ,
∴$\frac{KD}{QI}$=$\frac{KF}{PQ}$=2,∵∠FKD=∠PQH=90°,
∴△FKD∽△PQH,
∴∠FDK=∠QHP,
∵FO=OB,FH=HC,
∴BC=2OH,∵AF=BC=2OG,
∴OH=OG,易證OG=PO,
∴OG=OP=OH,以O為圓心OH為半徑作圓,
∵OJ⊥GP,OG=OP,
∴∠GOJ=∠POJ=∠OGM=∠GHP,
∵OG=OH,
∴∠OHG=∠OGH,
∵∠QHP=∠OHG+∠GHP=∠OGH+∠OGM=∠AGH,
∴∠AGH=∠ADF,
∵∠FAD=∠GAH(旋轉角相等),
∵AD=AF,
∴∠ADF=∠AFD,
∵∠FAD+∠ADF+∠AFD=180°,∠GAI+∠AGI+∠AIG=180°,
∴∠AIG=∠AFD=∠AGI,
∴AI=AG,
∵AE=AB,AG=GB,
∴AI=IE.
點評 本題考查四邊形綜合題、旋轉變換、矩形的性質、三角形中位線定理、等腰三角形的判定和性質等知識,解題的關鍵是學會利用參數解決問題,體現了數形結合的數學思想,本題輔助線比較多,發現△FKD∽△PQH,是解題的突破點,屬于競賽題.


科目:初中數學 來源: 題型:解答題
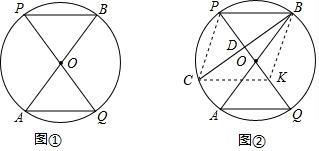
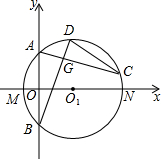 如圖,在平面直角坐標系中,直線y=2x+4交x軸于點M,交y軸于點A,過A,M兩點的⊙O1的圓心O1在x軸上,交x軸于另一點N,交y軸于另一點B,D,C為優弧$\widehat{AB}$上兩動點,且AC⊥BD交BD于G,延長OG交CD于H.
如圖,在平面直角坐標系中,直線y=2x+4交x軸于點M,交y軸于點A,過A,M兩點的⊙O1的圓心O1在x軸上,交x軸于另一點N,交y軸于另一點B,D,C為優弧$\widehat{AB}$上兩動點,且AC⊥BD交BD于G,延長OG交CD于H.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,⊙M與x軸交于A、B兩點,與y軸切于點C,且OA,OB的長是方程x2-4x+3=0的解.
如圖,⊙M與x軸交于A、B兩點,與y軸切于點C,且OA,OB的長是方程x2-4x+3=0的解.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系內,梯形OABC的頂點坐標分別是:A(3,4),B(8,4),C(11,0),點P(t,0)是線段OC上一點,設四邊形ABCP的面積為S.
如圖,在平面直角坐標系內,梯形OABC的頂點坐標分別是:A(3,4),B(8,4),C(11,0),點P(t,0)是線段OC上一點,設四邊形ABCP的面積為S.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com