
 如圖,⊙M與x軸交于A、B兩點,與y軸切于點C,且OA,OB的長是方程x2-4x+3=0的解.
如圖,⊙M與x軸交于A、B兩點,與y軸切于點C,且OA,OB的長是方程x2-4x+3=0的解.分析 (1)過點M作ME⊥x軸于點E,連接MC,解出方程后可知OA=1,OB=3,然后即可求出OE的長度,由于C是切點,所以MC是半徑,又因為MC=OE,從而可知⊙M的半徑,利用垂徑定理即可求出M的坐標.
(2)由于點P的位置不確定,需要分兩種情況進行討論,可根據圓周角定理以及圓內接四邊形的性質求解.
解答 解:(1)過點M作ME⊥x軸于點E,連接MC,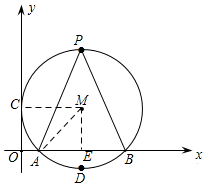
∵OA,OB的長是方程x2-4x+3=0的解,
∴解得x=1或x=3,
∴OA=1,OB=3,
∴A(1,0),B(3,0)
由垂徑定理可知:AE=BE,
∴E(2,0),
∴OE=2,AE=1,
∵⊙M與y軸切于點C,
∴MC是⊙M的半徑,
∴MC=OE=2,
∴由勾股定理可知:ME=$\sqrt{3}$,
∴M的坐標為(2,$\sqrt{3}$);
(2)連接MB、AM
當點P在x軸上方時,
由(1)可知:AM=2,AE=1,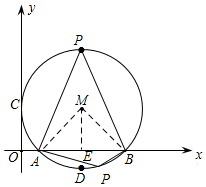
∴∠AME=30°,
∴由垂徑定理可知:∠AMB=60°,
∴由圓周角定理可知:∠APB=$\frac{1}{2}$∠AMB=30°,
當點P在x軸下方時,
∴由圓內接四邊形的性質可知:此時∠APB=180°-30°=150°
點評 本題考查圓的相關性質,解題的關鍵是根據OA與OB的長度,以及切點C求出⊙M的半徑,從而根據垂徑定理、勾股定理,圓周角定理求出M的坐標和∠APB的度數.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題

| 輸入 n | 3 | 2 | -1 | -2 | … |
| 輸出答案 | 3 | 2 | -1 | -2 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
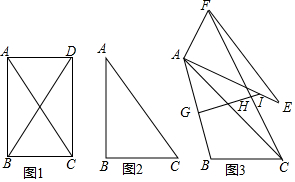
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
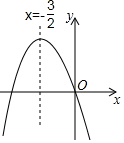 如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下四個結論:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正確的結論有( )
如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下四個結論:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正確的結論有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com