
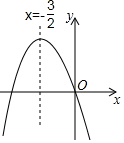 如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下四個結論:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正確的結論有( )
如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下四個結論:①abc=0;②a+b+c>0;③a>b;④b2-4ac<0;其中正確的結論有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 由拋物線開口方向得到a<0以及函數經過原點即可判斷①,由拋物線的對稱軸方程得到為b=2a<0,以及a的符號即可判斷③;根據x=1時的函數值可以判斷②;根據拋物線與x軸交點個數得到△=b2-4ac>0,則可對④進行判斷.
解答 解:∵拋物線開口向下,
∴a<0,
∵拋物線經過原點,
∴c=0,
則abc=0,所以①正確;
當x=1時,函數值是a+b+c<0,則②錯誤;
∵拋物線的對稱軸為直線x=-$\frac{b}{2a}$=-$\frac{3}{2}$<0,
∴b=3a<0,
又∵a<0,
∴a>b,則③正確;
∵拋物線與x軸有2個交點,
∴△=b2-4ac>0,所以④錯誤.
故選B.
點評 本題考查了二次函數圖象與系數的關系:對于二次函數y=ax2+bx+c(a≠0),二次項系數a決定拋物線的開口方向和大小:當a>0時,拋物線向上開口;當a<0時,拋物線向下開口;一次項系數b和二次項系數a共同決定對稱軸的位置:當a與b同號時(即ab>0),對稱軸在y軸左; 當a與b異號時(即ab<0),對稱軸在y軸右;常數項c決定拋物線與y軸交點位置:拋物線與y軸交于(0,c);拋物線與x軸交點個數由△決定:△=b2-4ac>0時,拋物線與x軸有2個交點;△=b2-4ac=0時,拋物線與x軸有1個交點;△=b2-4ac<0時,拋物線與x軸沒有交點.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
| 信息序號 | 文字信息 | 數學表達式 |
| 1 | C和D的得分之和是E得分的2倍 | C+D=2E |
| 2 | B的得分高于D | B>D |
| 3 | A和B的得分之和等于C和D的總分 | A+B=C+D |
| 4 | D的得分高于E | D>E |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,⊙M與x軸交于A、B兩點,與y軸切于點C,且OA,OB的長是方程x2-4x+3=0的解.
如圖,⊙M與x軸交于A、B兩點,與y軸切于點C,且OA,OB的長是方程x2-4x+3=0的解.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | SAS | B. | AAS | C. | ASA | D. | SSS |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,直線y1=kx+b與雙曲線y2=$\frac{m}{x}$交于A、B兩點,它們的橫坐標分別為1和5.
如圖,直線y1=kx+b與雙曲線y2=$\frac{m}{x}$交于A、B兩點,它們的橫坐標分別為1和5.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-4,2) | B. | (4,-2) | C. | (2,4) | D. | (-2,-4) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com