
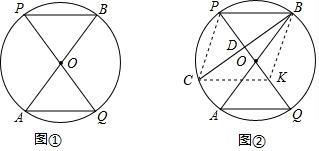
分析 (1)由同弧所對的圓周角相等得出∠P=∠A,由OA=OQ得出∠A=∠Q,那么∠P=∠Q,AQ∥PB.根據∠AOQ=∠BOP,得到$\widehat{AQ}$=$\widehat{BP}$,那么AQ=BP;
(2)先由垂徑定理得出BD=CD,又PD=DK,得出四邊形BKCP為菱形,根據菱形的性質得出PB∥CK,再證明CK∥AQ,且CK=AQ,那么四邊形AQKC為平行四邊形.
解答 證明:(1)∵$\widehat{BQ}$=$\widehat{BQ}$,
∴∠P=∠A,
∵OA=OQ,
∴∠A=∠Q,
∴∠P=∠Q,
∴AQ∥PB. ∵∠AOQ=∠BOP,
∵∠AOQ=∠BOP,
∴$\widehat{AQ}$=$\widehat{BP}$,
∴AQ=BP;
(2)∵PQ⊥BC,
∴BD=CD,
又∵PD=DK,
∴BC與PK互相垂直且平分,
∴四邊形BKCP為菱形;
∴PB∥CK,且PB=CK,
∵PB∥AQ,
∴CK∥AQ,
∵PB=AQ,
∴CK=AQ,
∵CK∥AQ,且CK=AQ,
∴四邊形AQKC為平行四邊形.
點評 本題考查了平行四邊形的判定,菱形的判定與性質,圓周角定理,關鍵是得出四邊形BKCP為菱形,難度適中.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
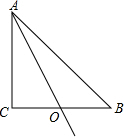 如圖,在△ABC中,∠ACB=90°,AC=BC=2,O是BC的中點,P是射線AO上的一個動點,則當∠BPC=90°時,AP的長為$\sqrt{5}$-1或$\sqrt{5}$+1.
如圖,在△ABC中,∠ACB=90°,AC=BC=2,O是BC的中點,P是射線AO上的一個動點,則當∠BPC=90°時,AP的長為$\sqrt{5}$-1或$\sqrt{5}$+1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com