
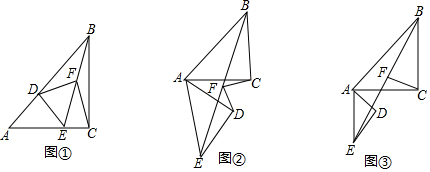
分析 (1)根據“直角三角形斜邊上的中線等于斜邊的一半”可知DF=BF,根據∠DFE=2∠DCF,∠BFE=2∠BCF,得到∠EFD+∠EFB=2∠DCB=90°,進而得出DF⊥BF;
(2)先過B作BG∥ED,交DF的延長線于G,連接CG,CD,則∠DEF=∠GBF,根據ASA判定△DEF≌△GBF,進而得出DE=GB=AD,且DF=GF,再根據角的和差關系得到∠DAC=∠CBG,進而判定△ACD≌△BCG(SAS),從而得出CD=CG,∠BCG=∠ACD,最后判定△CDG是等腰直角三角形,根據F是DG的中點,即可得出CF=$\frac{1}{2}$DG=DF,CF⊥DF;
(3)延長DF交BA于點H,先證明△DEF≌△HBF,得到DE=BH,DF=FH,根據旋轉條件可以△ADH為直角三角形,由△ABC和△ADE是等腰直角三角形,AC=2$\sqrt{2}$,可以求出AB的值為4,進而可以根據勾股定理可以求出DH為$\sqrt{10}$,再求出DF,由DF=CF,即可求得CF的值.
解答  解:(1)如圖1,∵∠ACB=∠ADE=90°,點F為BE中點,
解:(1)如圖1,∵∠ACB=∠ADE=90°,點F為BE中點,
∴DF=$\frac{1}{2}$BE,CF=$\frac{1}{2}$BE,
∴DF=CF.
∵△ABC和△ADE是等腰直角三角形,
∴∠ABC=45°
∵BF=DF,
∴∠DBF=∠BDF,
∵∠DFE=∠ABE+∠BDF,
∴∠DFE=2∠DBF,
同理,∠CFE=2∠CBF,
∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,
∴DF⊥CF;
(2)DF=CF,DF⊥CF仍成立.
理由:如圖2,過B作BG∥ED,交DF的延長線于G,連接CG,CD,則∠DEF=∠GBF,
∵點F為BE的中點,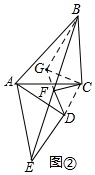
∴BF=EF,
在△DEF和△GBF中,
$\left\{\begin{array}{l}{∠DEF=∠GBF}\\{EF=BF}\\{∠DFE=∠GFB}\end{array}\right.$,
∴△DEF≌△GBF(ASA),
∴DE=GB=AD,且DF=GF,
∵△ABC為等腰直角三角形,
∴AC=BC,
∵△ABE中,∠BAE=180°-∠AEB-∠ABE,而∠BAC=∠EAD=45°,
∴∠DAC=∠BAE-∠BAC-∠EAD=(180°-∠AEB-∠ABE)-45°-45°=90°-∠AEB-∠ABE,
又∵∠ABE=∠ABC-CBE=45°-∠CBE,
∠AEB=∠AED-∠DEB=45°-∠DEB,
∴∠DAC=90°-(45°-∠DEB)-(45°-∠CBE)=∠DEB+∠CBE=∠GBE+∠CBE=∠CBG,
在△ACD和△BCG中,
$\left\{\begin{array}{l}{AD=BG}\\{∠DAC=∠GBC}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△BCG(SAS),
∴CD=CG,∠BCG=∠ACD,
又∵∠BCG+∠ACG=90°,
∴∠ACD+∠ACG=90°,
∴∠DCG=90°,
∴△CDG是等腰直角三角形,
∵F是DG的中點,
∴CF=$\frac{1}{2}$DG=DF,CF⊥DF;
(3)如圖3所示,延長DF交BA于點H,
∵△ABC和△ADE是等腰直角三角形,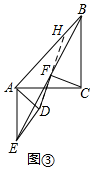
∴AC=BC,AD=DE.
∴∠AED=∠ABC=45°,
∵∠BAE=135°,
∴∠BAE+∠ABC=180°,且∠BAD=90°,
∴AE∥BC,
∴∠AEB=∠CBE,
∴∠DEF=∠HBF,
∵F是BE的中點,
∴EF=BF,
在△DEF和△HBF中,
$\left\{\begin{array}{l}{∠DEF=∠HBF}\\{∠DFE=∠HFB}\\{EF=BF}\end{array}\right.$,
∴△DEF≌△HBF(AAS),
∴ED=HB,DF=HF,
∵AC=2$\sqrt{2}$,
在Rt△ABC中,由勾股定理得AB=4,
∵AD=1,
∴ED=BH=1,
∴AH=3,
在Rt△HAD中,由勾股定理得DH=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴DF=$\frac{1}{2}$DH=$\frac{1}{2}$$\sqrt{10}$,
同理可得CF=DF,
∴CF=$\frac{\sqrt{10}}{2}$,
故答案為:$\frac{\sqrt{10}}{2}$.
點評 本題屬于三角形綜合題,主要考查了直角三角形斜邊上的中線的性質,等腰直角三角形的性質,全等三角形的判定與性質及勾股定理的運用.解題時需要作輔助線,構造全等三角形以及等腰直角三角形,運用等腰直角三角形的性質和全等三角形的性質及其判定定理是解題的關鍵.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y1<y2<y3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
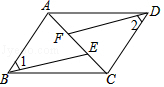 如圖,已知點A、F、E、C在同一直線上,AB∥CD,∠1=∠2,AF=CE.
如圖,已知點A、F、E、C在同一直線上,AB∥CD,∠1=∠2,AF=CE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 單位(千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐數 | 1 | 5 | 2 | 2 | 4 | 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
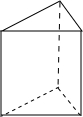 按要求完成下列各小題.
按要求完成下列各小題.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com