
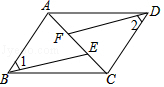
 如圖,已知點A、F、E、C在同一直線上,AB∥CD,∠1=∠2,AF=CE.
如圖,已知點A、F、E、C在同一直線上,AB∥CD,∠1=∠2,AF=CE.分析 (1)根據AB∥CD可得∠3=∠4,再根據AF=CE可得AE=CF,然后可利用AAS判定△ABE≌△CDF;由△ABE≌△CDF可得DF=BE,∠AEB=∠CFD,根據等角的補角相等可得∠AFD=∠BEC,然后可證明△AFD≌△CEB;
(2)根據AB∥CD可得∠3=∠4,再根據AF=CE可得AE=CF,然后可利用AAS判定△ABE≌△CDF.
解答 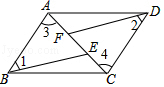 解:(1)△ABE≌△CDF;△AFD≌△CEB;
解:(1)△ABE≌△CDF;△AFD≌△CEB;
(2)∵AB∥CD,
∴∠3=∠4,
∵AF=CE,
∴AF+EF=CE+EF,
即AE=FC,
在△ABE和△CDF中$\left\{\begin{array}{l}{∠1=∠2}\\{∠3=∠4}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CDF(AAS).
點評 本題考查三角形全等的判定方法,判定兩個三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定兩個三角形全等,判定兩個三角形全等時,必須有邊的參與,若有兩邊一角對應相等時,角必須是兩邊的夾角.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:初中數學 來源: 題型:填空題
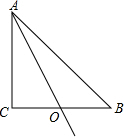 如圖,在△ABC中,∠ACB=90°,AC=BC=2,O是BC的中點,P是射線AO上的一個動點,則當∠BPC=90°時,AP的長為$\sqrt{5}$-1或$\sqrt{5}$+1.
如圖,在△ABC中,∠ACB=90°,AC=BC=2,O是BC的中點,P是射線AO上的一個動點,則當∠BPC=90°時,AP的長為$\sqrt{5}$-1或$\sqrt{5}$+1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com