

分析 (1)由正方形得對邊平行,由平行得△ADF∽△EBF,列比例式可得DF=2BF;
(2)如圖②,延長DC、AB交于M,先證明△CEM≌△BEA,CM=AB,即DM=2AB,再證明△DHM∽△GHA,列比例式可得結論;
(3)如圖③,作輔助線,構建相似三角形,同理證明△CGO≌△BGA,列比例式可得所求的比值.
解答  解:(1)如圖①,∵四邊形ABCD為正方形,
解:(1)如圖①,∵四邊形ABCD為正方形,
∴AD∥BC,AD=BC,
∵E是BC的中點,
∴BC=2BE,
∵AD∥BC,
∴△ADF∽△EBF,
∴$\frac{DF}{BF}=\frac{AD}{BE}$,
∴$\frac{DF}{BF}=\frac{BC}{BE}$=$\frac{2}{1}$,
∴DF=2BF;
故答案為:DF=2BF;
(2)如圖②,延長DC、AE交于M,
∵DC∥AB,
∴∠ABC=∠ECM,∠M=∠EAB,
∵CE=BE,
∴△CEM≌△BEA,
∴CM=AB,
∵G是AB的中點,
∴AG=BG,
設AG=x,則AB=2x,DM=4x,
∵DM∥AB,
∴△DHM∽△GHA,
∴$\frac{DM}{AG}=\frac{DH}{HG}$,
∴$\frac{4x}{x}$=$\frac{DH}{HG}$,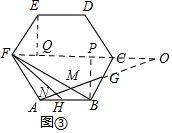
∴$\frac{DH}{HG}$=4;
(3)如圖③,連接FC并延長,交AG的延長線于O,過B作BP⊥OF于P,過E作EQ⊥OF于Q,
在正六邊形ABCDEF中,
∴∠ABC=180°-$\frac{360°}{6}$=120°,AB=BC,
∴∠PBC=120°-90°=30°,∠FCB+∠ABC=180°,
∴FC∥AB,PC=$\frac{1}{2}$BC,
同理FQ=$\frac{1}{2}$EF,
∵點H、G分別是AB、BC的中點,
∴AH=BH=$\frac{1}{2}$AB,BG=CG=$\frac{1}{2}$BC,
設AH=x,則BC=AB=2x,
∴FC=4x,
∵FC∥AB,
∴∠O=∠GAB,
∵BG=CG,∠CGO=∠BGA,
∴△CGO≌△BGA,
∴CO=AB=2x,
∴OF=6x,
∵OF∥AB,
∴△FNO∽△HNA,
∴$\frac{FN}{NH}=\frac{OF}{AH}$=$\frac{6x}{x}$,
∴$\frac{FN}{NH}$=6.
點評 本題是四邊形的綜合題,考查了正方形、正六邊形的性質、平行相似的判定,本題的關鍵是作輔助線,構建平行相似的三角形;同時還運用了類比的思想,通過問題1的解決,啟發了第2個和第3個問題的思路,利用作輔助線的方式使問題得以解決.


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
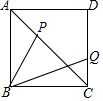 如圖,正方形ABCD中,已知AB=2,動點P、Q分別在AC、CD上,且AP=CQ,則(BP+BQ)2的最小值是8+4$\sqrt{2}$.
如圖,正方形ABCD中,已知AB=2,動點P、Q分別在AC、CD上,且AP=CQ,則(BP+BQ)2的最小值是8+4$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
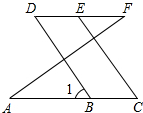 完成下列推理說明:
完成下列推理說明:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com