
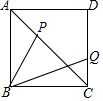
 如圖,正方形ABCD中,已知AB=2,動點P、Q分別在AC、CD上,且AP=CQ,則(BP+BQ)2的最小值是8+4$\sqrt{2}$.
如圖,正方形ABCD中,已知AB=2,動點P、Q分別在AC、CD上,且AP=CQ,則(BP+BQ)2的最小值是8+4$\sqrt{2}$. 分析 作輔助線,構(gòu)建一直線與BP相等,找到(BP+BQ)2的最小值時點Q的位置,先證明△ABP≌△CFQ,則BP=FQ,發(fā)現(xiàn)當B、Q、F三點共線時,BQ+FQ最小,即BP+BQ最小,利用勾股定理求出BF2即可.
解答 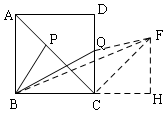 解:過C作CF⊥AC,使CF=AB,連接FQ、BF,
解:過C作CF⊥AC,使CF=AB,連接FQ、BF,
∵四邊形ABCD為正方形,
∴∠BAC=∠ACD=45°,
∴∠QCF=90°-45°=45°,
∴∠BAC=∠QCF=45°,
∵AB=CF,AP=CQ,
∴△ABP≌△CFQ,
∴BP=FQ,
∴BP+BQ=FQ+BQ≥BF,
當B、Q、F三點共線時,BQ+FQ最小,即BP+BQ最小,
此時過F作FH⊥BC,交BC的延長線于H,
∵∠DCH=90°,∠QCF=45°,
∴∠FCH=45°,
∵∠CHF=90°,
∴△CFH是等腰直角三角形,
∵CF=AB=2,
∴CH=FH=$\sqrt{2}$,
在Rt△BFH中,BF2=BH2+FH2=(2+$\sqrt{2}$)2+($\sqrt{2}$)2=8+4$\sqrt{2}$,
∴(BP+BQ)2的最小值是8+4$\sqrt{2}$;
故答案為:8+4$\sqrt{2}$.
點評 本題考查了正方形的性質(zhì)和最短路徑問題,作輔助線,構(gòu)建全等三角形,將線段BP轉(zhuǎn)化到線段FQ上是本題的關(guān)鍵,利用了三角形的三邊關(guān)系和勾股定理解決此題.


科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
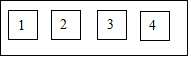 四張形狀相同的卡片如圖所示.將卡片洗勻后背面朝上放置在桌面上,小明先隨機抽取一張卡片,記下數(shù)字為x,小亮再隨機抽取一張卡片,記下數(shù)字為y.兩人在此基礎(chǔ)上共同協(xié)商一個游戲規(guī)則:當x>y時小明獲勝,否則小亮獲勝.
四張形狀相同的卡片如圖所示.將卡片洗勻后背面朝上放置在桌面上,小明先隨機抽取一張卡片,記下數(shù)字為x,小亮再隨機抽取一張卡片,記下數(shù)字為y.兩人在此基礎(chǔ)上共同協(xié)商一個游戲規(guī)則:當x>y時小明獲勝,否則小亮獲勝.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com