
 如圖是一個(gè)常見鐵夾的側(cè)面示意圖,OA、OB表示鐵夾的兩個(gè)葉片,C是軸,CD⊥OA于點(diǎn)D,已知DA=40mm,DO=35mm,DC=10mm,我們知道鐵夾的側(cè)面是軸對稱圖形,請求出A、B兩點(diǎn)間的距離.
如圖是一個(gè)常見鐵夾的側(cè)面示意圖,OA、OB表示鐵夾的兩個(gè)葉片,C是軸,CD⊥OA于點(diǎn)D,已知DA=40mm,DO=35mm,DC=10mm,我們知道鐵夾的側(cè)面是軸對稱圖形,請求出A、B兩點(diǎn)間的距離. 分析 先根據(jù)題意畫出圖形,再根據(jù)軸對稱的性質(zhì)求出Rt△OCD∽Rt△OAE,再根據(jù)相似三角形的對應(yīng)邊成比例及勾股定理求出AB的長即可.
解答 解:作出示意圖,
連接AB,同時(shí)連接OC并延長交AB于E,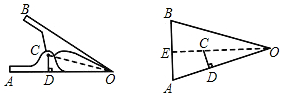
因?yàn)閵A子是軸對稱圖形,故OE是對稱軸,
∴OE⊥AB,AE=BE,
∵∠COD=∠AOE,∠CDO=∠AEO=90°,
∴Rt△OCD∽Rt△OAE,
∴$\frac{OC}{OA}$=$\frac{CD}{AE}$,
而OC=$\sqrt{C{D}^{2}+O{D}^{2}}$=$\sqrt{1{0}^{2}+3{5}^{2}}$=5$\sqrt{53}$,
即 $\frac{5\sqrt{53}}{75}$=$\frac{10}{AE}$,
∴AE=$\frac{150\sqrt{53}}{53}$,
∴AB=2AE=$\frac{300\sqrt{53}}{53}$(mm).
答:AB兩點(diǎn)間的距離為$\frac{300\sqrt{53}}{53}$mm.
點(diǎn)評 本題考查相似三角形的判定和性質(zhì)、軸對稱圖形、勾股定理等知識,解答此題的關(guān)鍵是根據(jù)題意畫出圖形,學(xué)會添加常用輔助線,構(gòu)造相似三角形解決問題,屬于中考常考題型.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
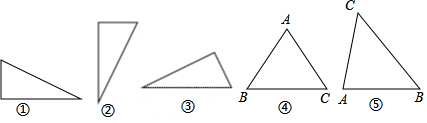
| 圖形 | 圖① | 圖② | 圖③ | 圖④ | 圖⑤ |
| 絕對高度 | 1.50 | 2.00 | 1.20 | 2.40 | ? |
| 絕對寬度 | 2.00 | 1.50 | 2.50 | 3.60 | ? |
| A. | 3.60和2.40 | B. | 2.56和3.00 | C. | 2.56和2.88 | D. | 2.88和3.00 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
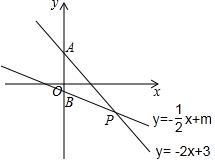 如圖,函數(shù)y=-2x+3與y=-$\frac{1}{2}$x+m的圖象交于P(n,-2).
如圖,函數(shù)y=-2x+3與y=-$\frac{1}{2}$x+m的圖象交于P(n,-2).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com