Question

10．如圖，已知一次函數y=x+2的圖象交y軸于點A，交x軸于點B，點E在x軸正半軸上，點F在射線BA上，且OE=OF=10．FH垂直x軸于點H．
（1）點E坐標為（10，0），點F坐標為（6，8）．
（2）操作：將一足夠大的三角板的直角頂點Q放在射線AF或射線HF上，一直角邊始終過點E，另一直角邊與y軸相交于點P．問是否存在這樣的點Q，使以點P，Q，E為頂點的三角形與△POE全等？若存在，求出點Q的坐標；若不存在，請說明理由．

Answer 1

分析 （1）根據點E在x軸正半軸上，OE=OF=10，即可得出E（10，0），再根據點F在射線BA上，可設F（x，x+2），則OH-x，FH=x+2，最后根據勾股定理求得x即可；
（2）當點Q在射線HF上時，分兩種情況：①QE=OE=10，②QP=OE=10；當點Q在射線AF上時，分兩種情況：①QE=OE=10，②QP=OE=10，分別作輔助線構造直角三角形或相似三角形，求得QH的長，即可得出點Q的坐標．

解答 解：（1）∵點E在x軸正半軸上，OE=OF=10，
∴E（10，0），
∵點F在射線BA上，
∴可設F（x，x+2），則OH-x，FH=x+2，
如圖，連接OF，則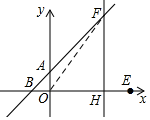

Rt△OHF中，x²+（x+2）²=10²，
解得x=6，
∴x+2=8，
∴F（6，8），
故答案為：（10，0），（6，8）；

（2）存在這樣的點Q，使以點P，Q，E為頂點的三角形與△POE全等．
當點Q在射線HF上時，分兩種情況：
①如圖所示，若QE=OE=10，而HE=10-6=4，
∴在Rt△QHE中，QH=$\sqrt{Q{E}^{2}-H{E}^{2}}$=$\sqrt{1{0}^{2}-{4}^{2}}$=2$\sqrt{21}$，
∴Q（6，2$\sqrt{21}$）；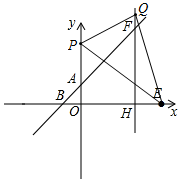

②如圖所示，若QP=OE=10，作PK⊥FH于K，則∠PKQ=∠QHE=90°，QK=$\sqrt{1{0}^{2}-{6}^{2}}$=8，
∵∠PQK+∠EQH=∠QEH+∠EQH=90°，
∴∠PQK=∠QEH，
∴△PQK∽△QEH，
∴$\frac{QH}{PK}$=$\frac{EH}{KQ}$，即$\frac{QH}{6}$=$\frac{4}{8}$，
解得QH=3，
∴Q（6，3）；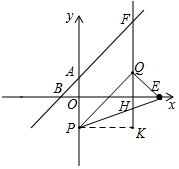


當點Q在射線AF上時，分兩種情況：
①如圖所示，若QE=OE=10，設Q（x，x+2），
作QR⊥x軸于R，則RE=10-x，QR=x+2，
∴Rt△QRE中，（10-x）²+（x+2）²=10²，
解得x=4±$\sqrt{14}$，
∴Q（4+$\sqrt{14}$，6+$\sqrt{14}$）或（4-$\sqrt{14}$，6-$\sqrt{14}$）；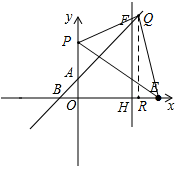

②如圖所示，若QP=OE=10，則QE=OP，
設Q（x，x+2），
∵∠POE=90°，
∴四邊形OPQE是矩形，
∴x=OE=10，
∵Q在射線AF上，
∴x+2=QE=12，
∴Q（10，12）．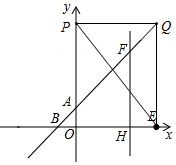

點評 本題屬于一次函數綜合題，主要考查了一次函數的圖象與性質，相似三角形的性質，矩形的性質以及勾股定理的綜合應用．解決第（2）題的關鍵是分類討論，運用勾股定理以及相似三角形的對應邊成比例進行計算求解．分類時注意不能遺漏，也不能重復．