
分析 (1)根據(jù)所給等式的變化規(guī)律可得a6=$\frac{8}{6×7{×2}^{7}}$=$\frac{1}{6{×2}^{6}}$-$\frac{1}{7{×2}^{7}}$;
(2)根據(jù)所給等式的變化規(guī)律可得an=$\frac{n+2}{n(n+1){•2}^{n+1}}$=$\frac{1}{{n•2}^{n}}-\frac{1}{(n+1){•2}^{n+1}}$.
解答 解:(1)∵第一個(gè)等式:a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$;
第二個(gè)等式:a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$,
第三個(gè)等式:a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$,
第四個(gè)等式:a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$,
∴第六個(gè)等式:a6=$\frac{8}{6×7{×2}^{7}}$=$\frac{1}{6{×2}^{6}}$-$\frac{1}{7{×2}^{7}}$;
(2)根據(jù)規(guī)律知:第n個(gè)等式:an=$\frac{n+2}{n(n+1){•2}^{n+1}}$=$\frac{1}{{n•2}^{n}}-\frac{1}{(n+1){•2}^{n+1}}$.
故答案為:$\frac{8}{6×7{×2}^{7}}$=$\frac{1}{6{×2}^{6}}-\frac{1}{7{×2}^{7}}$;$\frac{n+2}{n(n+1){•2}^{n+1}}$=$\frac{1}{{n•2}^{n}}-\frac{1}{(n+1){•2}^{n+1}}$.
點(diǎn)評(píng) 本題主要考查了數(shù)字的變化規(guī)律,發(fā)現(xiàn)規(guī)律,運(yùn)用規(guī)律是解答此題的關(guān)鍵.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
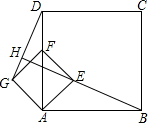 四邊形ABCD、AEFG都是正方形,當(dāng)正方形AEFG繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)45°時(shí),如圖,連接DG、BE,并延長BE交DG于點(diǎn)H,且BH⊥DG與H,若AB=4,AE=$\sqrt{2}$時(shí),則線段BH的長是( )
四邊形ABCD、AEFG都是正方形,當(dāng)正方形AEFG繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)45°時(shí),如圖,連接DG、BE,并延長BE交DG于點(diǎn)H,且BH⊥DG與H,若AB=4,AE=$\sqrt{2}$時(shí),則線段BH的長是( )| A. | $4\sqrt{2}$ | B. | 16 | C. | $\frac{{8\sqrt{10}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3個(gè) | B. | 2個(gè) | C. | 1 | D. | 0個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,E是正方形ABCD對(duì)角線BD上一點(diǎn),EM⊥BC,EN⊥CD垂足分別是求M、N
如圖,E是正方形ABCD對(duì)角線BD上一點(diǎn),EM⊥BC,EN⊥CD垂足分別是求M、N查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2、3、$\sqrt{5}$ | B. | 8、15、17 | C. | 0.6、0.8、1 | D. | $\sqrt{5}$、$\sqrt{12}$、$\sqrt{13}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 將長為30cm寬為10cm的長方形白紙,按如圖方法粘合起來,粘合部分的寬度為3cm
將長為30cm寬為10cm的長方形白紙,按如圖方法粘合起來,粘合部分的寬度為3cm查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com