
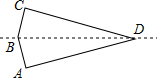
 如圖,在四邊形紙片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°,將紙片先沿直線BD對折,再將對折后的圖形沿從一個頂點出發的直線裁剪,剪開后的圖形打開鋪平,若鋪平后的圖形中有一個是面積為2的平行四邊形,則BC=2或1.
如圖,在四邊形紙片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°,將紙片先沿直線BD對折,再將對折后的圖形沿從一個頂點出發的直線裁剪,剪開后的圖形打開鋪平,若鋪平后的圖形中有一個是面積為2的平行四邊形,則BC=2或1. 分析 根據題意結合裁剪的方法得出符合題意的圖形有兩個,分別利用菱形的判定與性質得出CB的長.
解答 解:如圖1所示:作AE∥BC,延長AE交CD于點N,過點B作BT⊥EC于點T,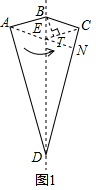
當四邊形ABCE為平行四邊形,
∵AB=BC,
∴四邊形ABCE是菱形,
∵∠A=∠C=90°,∠B=150°,BC∥AN,
∴∠ADC=30°,∠BAN=∠BCE=30°,
則∠NAD=60°,
∴∠AND=90°,
∵四邊形ABCE面積為2,
∴設BT=x,則BC=EC=2x,
故2x×x=2,
解得:x=1(負數舍去),
故BC=2;
如圖2,當四邊形BEDF是平行四邊形,
∵BE=BF,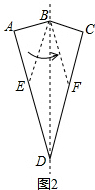
∴平行四邊形BEDF是菱形,
∵∠A=∠C=90°,∠B=150°,
∴∠ADB=∠BDC=15°,
∵BE=DE,
∴∠AEB=30°,
∴設AB=y,則BE=2y,
∵四邊形BEDF面積為2,
∴AB×DE=2y2=2,
解得:y=1,
故BC=1,
綜上所述:BC=2或1.
故答案為:2或1.
點評 此題主要考查了剪紙問題以及勾股定理和平行四邊形的性質等知識,根據題意畫出正確圖形是解題關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
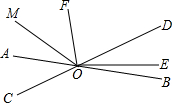 如圖,直線AB,CD相交于點O,∠DOE:∠BOE=3:1,OF平分∠AOD,
如圖,直線AB,CD相交于點O,∠DOE:∠BOE=3:1,OF平分∠AOD,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com