
分析 (1)設銷售單價x元,利潤為w元.由題意w=(x-6)[200-20(x-10)],利用二次函數的性質即可解決問題.
(2)分別求出兩種方案利潤的最大值,即可判斷.
解答 解:(1)設銷售單價x元,利潤為w元.
由題意w=(x-6)[200-20(x-10)]=-20(x-13)2+5780.
∵-20<0,
∴x=13時,每天的銷售利潤最大,
∴銷售單價為13元時,“孝心襪”每天的銷售利潤最大.
(2)方案A:“孝心襪”的銷售單價高于進價且不超過11元;
∵w=(x-6)[200-20(x-10)]=-20(x-13)2+5780.
又∵6<x≤11,
∴x=11時,w的值最大,最大值為5740元.
方案B:每天銷售量不少于20雙,且每雙“孝心襪”的利潤至少為10元.
∵w=(x-6)[200-20(x-10)]=-20(x-13)2+5780.
又∵16≤x≤19,
∴x=16時,w的值最大,最大值為5600元.
∵5740<5600,
∴方案A的利潤最大.
點評 本題考查了二次函數的應用、一元二次方程的應用等知識,最大銷售利潤的問題常利用函數的增減性來解答,我們首先要吃透題意,確定變量,建立函數模型,然后結合實際選擇最優方案.其中要注意應該在自變量的取值范圍內求最大值(或最小值),也就是說二次函數的最值不一定在x=$\frac{b}{2a}$時取得.


 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
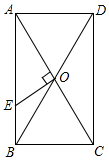 如圖,已知矩形ABCD的對角線AC、BD相交于點O,過O點作OE⊥AC,交AB于E,若BC=4,△AOE的面積是5,則下列說法錯誤的是( )
如圖,已知矩形ABCD的對角線AC、BD相交于點O,過O點作OE⊥AC,交AB于E,若BC=4,△AOE的面積是5,則下列說法錯誤的是( )| A. | AE=5 | B. | ∠BOE=∠BCE | C. | CE⊥OB | D. | sin∠BOE=$\frac{3}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com