
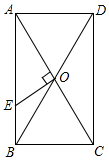
 如圖,已知矩形ABCD的對(duì)角線AC、BD相交于點(diǎn)O,過O點(diǎn)作OE⊥AC,交AB于E,若BC=4,△AOE的面積是5,則下列說法錯(cuò)誤的是( )
如圖,已知矩形ABCD的對(duì)角線AC、BD相交于點(diǎn)O,過O點(diǎn)作OE⊥AC,交AB于E,若BC=4,△AOE的面積是5,則下列說法錯(cuò)誤的是( )| A. | AE=5 | B. | ∠BOE=∠BCE | C. | CE⊥OB | D. | sin∠BOE=$\frac{3}{5}$ |
分析 A、作輔助線,構(gòu)建矩形AGOF,利用面積為5,代入面積公式可求得AE的長為5,此說法正確;
B、證明∠ABC+∠EOC=180°,根據(jù)對(duì)角互補(bǔ)的四邊形四點(diǎn)共圓得:E、B、C、O四點(diǎn)共圓,則∠BCE=∠BOE,此說法正確;
C、因?yàn)镋、B、C、O四點(diǎn)共圓,所以根據(jù)垂徑定理可知:要想OB⊥CE,得保證過圓心的直線平分弧,即判斷弦長BE和OE的大小即可;
D、利用同角的三角函數(shù)計(jì)算.
解答 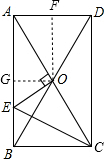 解:A、過O作OF⊥AD于F,作OG⊥AB于G,
解:A、過O作OF⊥AD于F,作OG⊥AB于G,
∵四邊形ABCD是矩形,
∴AC=BD,OA=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,
∴OA=OD,
∴AF=FD=$\frac{1}{2}$AD=$\frac{1}{2}$BC=2,
∵∠AGO=∠BAD=∠AFO=90°,
∴四邊形AGOF是矩形,
∴OG=AF=2,
∵S△AEO=$\frac{1}{2}$AE•OG=5,
∴AE=$\frac{10}{OG}$=$\frac{10}{2}$=5,
所以此選項(xiàng)的說法正確;
B、∵OE⊥AC,
∴∠EOC=90°
∵∠ABC=90°,
∴∠ABC+∠EOC=180°,
∴E、B、C、O四點(diǎn)共圓,
∴∠BCE=∠BOE,
所以此選項(xiàng)的說法正確;
C、在Rt△BEC中,由勾股定理得:BE=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AB=3+5=8,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴AO=$\frac{1}{2}$AC=2$\sqrt{5}$,
∴EO=$\sqrt{A{E}^{2}-A{O}^{2}}$=$\sqrt{{5}^{2}-(2\sqrt{5})^{2}}$=$\sqrt{5}$,
∴OE≠BE,
∵E、B、C、O四點(diǎn)共圓,
∵∠EOC=90°,
∴EC是直徑,
∴EC與OB不垂直;
此選項(xiàng)的說法不正確;
D、sin∠BOE=sin∠BCE=$\frac{BE}{EC}$=$\frac{3}{5}$,
所以此選項(xiàng)的說法正確,
因?yàn)楸绢}選擇說法錯(cuò)誤的,
故選C.
點(diǎn)評(píng) 本題考查了矩形的性質(zhì)和判定、四點(diǎn)共圓的判定和性質(zhì)、勾股定理以及解直角三角形的有關(guān)知識(shí),較為麻煩,此類題相當(dāng)于解決四個(gè)問題,尤其是第三問利用了圓中的性質(zhì)進(jìn)行證明,比較容易理解;本題還利用了同角的三角函數(shù)求一個(gè)角的正弦,這在解直角三角形中經(jīng)常運(yùn)用,要熟練掌握.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
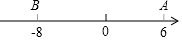 已知數(shù)軸上兩點(diǎn)A、B對(duì)應(yīng)的數(shù)分別是6,-8,M、N為數(shù)軸上兩個(gè)動(dòng)點(diǎn),點(diǎn)M從A點(diǎn)出發(fā)向左運(yùn)動(dòng),速度為每秒2個(gè)單位長度,與此同時(shí),點(diǎn)N從B點(diǎn)出發(fā)向右運(yùn)動(dòng),速度為M點(diǎn)的3倍,經(jīng)過多長時(shí)間,點(diǎn)M與點(diǎn)N相距50個(gè)單位長度?這時(shí)點(diǎn)M、N所對(duì)應(yīng)的數(shù)分別是多少?
已知數(shù)軸上兩點(diǎn)A、B對(duì)應(yīng)的數(shù)分別是6,-8,M、N為數(shù)軸上兩個(gè)動(dòng)點(diǎn),點(diǎn)M從A點(diǎn)出發(fā)向左運(yùn)動(dòng),速度為每秒2個(gè)單位長度,與此同時(shí),點(diǎn)N從B點(diǎn)出發(fā)向右運(yùn)動(dòng),速度為M點(diǎn)的3倍,經(jīng)過多長時(shí)間,點(diǎn)M與點(diǎn)N相距50個(gè)單位長度?這時(shí)點(diǎn)M、N所對(duì)應(yīng)的數(shù)分別是多少?查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 互余 | B. | 互補(bǔ) | ||
| C. | 既不互余也不互補(bǔ) | D. | 不確定 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
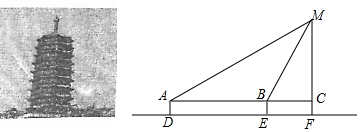
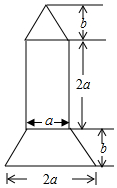 2016年9月15日晚,正值中秋佳節(jié),我國“天宮二號(hào)”空間實(shí)驗(yàn)室順利升空,這意味著中國載人航天工程將擁有首個(gè)真正意義的空間實(shí)驗(yàn)室.同學(xué)們倍受鼓舞,如圖是某同學(xué)繪制的火箭模型截面圖,上面是三角形,中間是長方形,下面是梯形,.
2016年9月15日晚,正值中秋佳節(jié),我國“天宮二號(hào)”空間實(shí)驗(yàn)室順利升空,這意味著中國載人航天工程將擁有首個(gè)真正意義的空間實(shí)驗(yàn)室.同學(xué)們倍受鼓舞,如圖是某同學(xué)繪制的火箭模型截面圖,上面是三角形,中間是長方形,下面是梯形,.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 兩點(diǎn)確定一條直線 | B. | 兩點(diǎn)確定一條線段 | ||
| C. | 兩點(diǎn)之間線段最短 | D. | 兩點(diǎn)之間直線最短 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
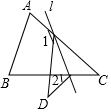 如圖,在△ABC中,∠C=40°,將△ABC沿著直線l折疊,點(diǎn)C落在點(diǎn)D的位置,則∠1-∠2的度數(shù)是( )
如圖,在△ABC中,∠C=40°,將△ABC沿著直線l折疊,點(diǎn)C落在點(diǎn)D的位置,則∠1-∠2的度數(shù)是( )| A. | 140° | B. | 90° | C. | 80° | D. | 40° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com