
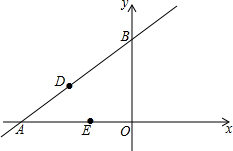
 在平面直角坐標系xOy中,A(-8,0),B(0,6),點D、E同時從A點出發,其中點D沿射線AB運動,速度為每秒4個單位;點E沿射線AO運動,速度為每秒5個單位.
在平面直角坐標系xOy中,A(-8,0),B(0,6),點D、E同時從A點出發,其中點D沿射線AB運動,速度為每秒4個單位;點E沿射線AO運動,速度為每秒5個單位.分析 (1)易證AO,BO的長,由勾股定理即可求出AB的長;
(2)以ED為半徑的⊙E與直線AB相切,易證△ADE∽△AOB,由相似三角形的性質可得:∠ADE=∠AOB=90°,進而可證明⊙E與直線AB相切;
(3)因為⊙E是動圓,所以當⊙E與y軸及直線CF都相切時有兩種情況:①當⊙E在y軸的左側與y軸相切;②當⊙E在y軸的右左側與y軸相切,再就兩種情況分別討論求出符合題意的t值即可.
解答 解:(1)∵A(-8,0),B(0,6),
∴AO=8,BO=6,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
故答案為:10;
(2)始終相切,理由如下:
由題意得:AD=4t,AE=5t,
∴$\frac{AD}{AE}=\frac{4}{5}=\frac{AO}{AB}$,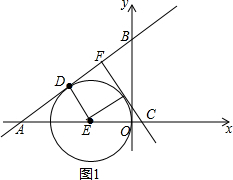
又∵∠DAE=∠OAB,
∴△ADE∽△AOB,
∴∠ADE=∠AOB=90°,
∵點D在AB上,
∴⊙E在運動過程中保持與AB相切;
(3)①當⊙E在y軸的左側與y軸相切時,如圖1,DE=OE,3t=8-5t,t=1,
此時,AE=5,AD=4,DE=3,
∵△ADE∽△AOB,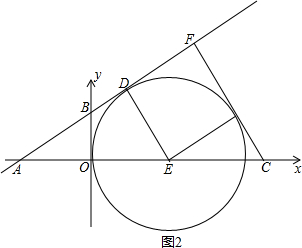
∴$\frac{AE}{AC}=\frac{AD}{AF}$,
當⊙E在y軸及CF都相切時,DF=DE,
∴$\frac{5}{8+m}=\frac{4}{4+3}$
解得$m=\frac{3}{4}$;
②當⊙E在y軸的右左側與y軸相切時,如圖2,DE=OE,3t=5t-8,t=4,此時,AE=20,AD=16,DE=12,
∵△ADE∽△AOB,
∴$\frac{AE}{AC}=\frac{AD}{AF}$,
當⊙E在y軸及CF都相切時,DF=DE,
∴$\frac{20}{8+m}=\frac{16}{16+12}$,
解得m=27.
綜上可知當t=1、m=$\frac{3}{4}$或t=4、m=27時滿足題意.
點評 本題考查了和圓有關的綜合性題目,用到的知識點有切線的性質定理、切線的判定定理、相似三角形的判定和性質以及勾股定理的運用,正確運用數形結合思想與分類討論思想是解題的關鍵.


科目:初中數學 來源: 題型:解答題
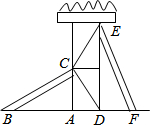 某游樂場有兩個長度相同的滑梯,要想使左邊滑梯BC的高度AC與右邊滑梯EF的水平方向的長度DF相等,則兩個滑梯的傾斜角∠ABC與∠DFE的大小必須滿足什么關系?說明理由.
某游樂場有兩個長度相同的滑梯,要想使左邊滑梯BC的高度AC與右邊滑梯EF的水平方向的長度DF相等,則兩個滑梯的傾斜角∠ABC與∠DFE的大小必須滿足什么關系?說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
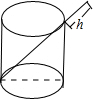 將一根26cm的筷子,置于底面直徑為9cm,高12cm的圓柱形水杯中,如圖所示,設筷子露在杯子外面的長度為hcm,則h的最小值是11cm.
將一根26cm的筷子,置于底面直徑為9cm,高12cm的圓柱形水杯中,如圖所示,設筷子露在杯子外面的長度為hcm,則h的最小值是11cm.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
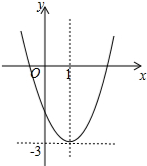 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正確結論的個數是( )
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正確結論的個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m=2,n=3 | B. | m=1,n=2 | C. | m=1,n=3 | D. | m=2,n=2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:拋物線y1=x2+bx+3與x軸分別交于點A(-3,0),B(m,0).將y1向右平移4個單位得到y2.
已知:拋物線y1=x2+bx+3與x軸分別交于點A(-3,0),B(m,0).將y1向右平移4個單位得到y2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com