
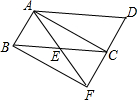
 如圖,已知點E是?ABCD中BC邊的中點,連接AE并延長交DC的延長線于點F.
如圖,已知點E是?ABCD中BC邊的中點,連接AE并延長交DC的延長線于點F.分析 (1)由ABCD為平行四邊形,根據(jù)平行四邊形的對邊平行得到AB與DC平行,根據(jù)兩直線平行內(nèi)錯角相等得到一對角相等,由E為BC的中點,得到兩條線段相等,再由對應角相等,利用ASA可得出三角形ABE與三角形FCE全等;進而得出AB=FC,即可得出四邊形ABFC是平行四邊形,再由直角三角形的判定方法得出△BFC是直角三角形,即可得出平行四邊形ABFC是矩形.
(4)由等邊三角形的性質(zhì)得出∠AFC=60°,AF=DF=4,得出CF=CD=2,由矩形的性質(zhì)得出∠ACF=90°,得出AC=$\sqrt{3}$CF=2$\sqrt{3}$,即可得出四邊形ABFC的面積=AC•CF=4$\sqrt{3}$.
解答 (1)證明:∵四邊形ABCD為平行四邊形,
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E為BC的中點
∴BE=CE,
在△ABE和△FCE中,$\left\{\begin{array}{l}{∠ABE=∠ECF}&{\;}\\{BE=CF}&{\;}\\{∠AEB=∠FEC}&{\;}\end{array}\right.$,
∴△ABE≌△FCE(ASA);
∴AE=EF,AB=CF,
∴四邊形ABFC是平行四邊形,
∵∠AEC=2∠ABC=∠ABC+∠BAE,
∴∠ABC=BAE,
∴AE=BE
∵AE=EF,BE=CE,
∴AF=BC
∴平行四邊形ABFC是矩形.
(2)解:∵△AFD是等邊三角形,
∴∠AFC=60°,AF=DF=4,
∴CF=CD=2,
∵四邊形ABFC是矩形,
∴∠ACF=90°,
∴AC=$\sqrt{3}$CF=2$\sqrt{3}$,
∴四邊形ABFC的面積=AC•CF=4$\sqrt{3}$.
點評 此題主要考查了矩形的判定以及全等三角形的判定與性質(zhì)等知識,根據(jù)已知得出AB=CF是解題關(guān)鍵.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數(shù)學 來源: 題型:選擇題
| A. | 小王合算 | B. | 小李合算 | ||
| C. | 一樣合算 | D. | 無法確定誰更合算 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| 運行區(qū)間 | 公布票價 | 學生票 | ||
| 上車站 | 下車站 | 一等座 | 二等座 | 二等座 |
| 長沙 | 井岡山 | 81(元) | 68(元) | 51(元) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,有一條小路穿過長方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,則這條小路AECF的面積是多少?
如圖,有一條小路穿過長方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,則這條小路AECF的面積是多少?查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| 路程(千米) | 運費(元/噸.千米) | |||
| 甲倉庫 | 乙倉庫 | 甲倉庫 | 乙倉庫 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
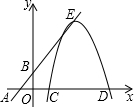 如圖,一次函數(shù)y=x+2與x軸交于點A,與y軸交于點B,一拋物線的頂點在直線AB上,形狀與函數(shù)y=-$\frac{1}{2}$x2圖象相同,它與x軸分別交于點C、D(點C在點D的左側(cè)),拋物線的頂點為點E.
如圖,一次函數(shù)y=x+2與x軸交于點A,與y軸交于點B,一拋物線的頂點在直線AB上,形狀與函數(shù)y=-$\frac{1}{2}$x2圖象相同,它與x軸分別交于點C、D(點C在點D的左側(cè)),拋物線的頂點為點E.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com