
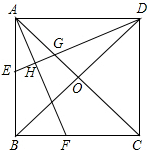
 已知,如圖,在正方形ABCD中,O是對角線的交點,AF平分∠BAC,DH⊥AF于點H,交AC于點G,DH延長線交AB于點E.
已知,如圖,在正方形ABCD中,O是對角線的交點,AF平分∠BAC,DH⊥AF于點H,交AC于點G,DH延長線交AB于點E.分析 作OM∥AB交DE于M.首先證明OM是△DEB的中位線,再證明OG=OM即可解決問題.
解答 解:作OM∥AB交DE于M.
∵四邊形ABCD是正方形,
∴OB=OD,
∵OH∥BE,
∴EM=DM,
∴BE=2OM,
∵∠OAD=∠ADO=∠BAC=45°,
∵FA平分∠BAC,
∴∠EAH=22.5°,
∵AF⊥DE,
∴∠AHE=∠AHD=90°,
∴∠AEH=67.5°,
∵∠ADE+∠AED=90°,
∴∠ADE=22.5°,
∴∠OGD=∠GAD+∠ADE=67.5°,
∵∠AEH=∠OME=67.5°,
∴∠OGM=∠OMG,
∴OG=OM,
∴BE=2OG.
點評 本題考查正方形的性質、三角形的中位線定理、角平分線的定義、等腰三角形的判定和性質等知識,解題的關鍵是學會添加輔助線,構造三角形中位線解決問題,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
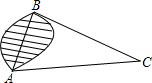 如圖,為了求出湖兩岸的A、B點之間的距離,一個觀測者在點C設樁,使三角形ABC恰好為直角三角形,通過測量,得到AC長160米,BC長128米,問從點A穿過湖到點B有多遠?
如圖,為了求出湖兩岸的A、B點之間的距離,一個觀測者在點C設樁,使三角形ABC恰好為直角三角形,通過測量,得到AC長160米,BC長128米,問從點A穿過湖到點B有多遠?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在△ABC中,AD是BC邊上的中線,E是AD的中點,連接BE并延長交AC于點F,G是BF的中點.求證:
如圖,已知在△ABC中,AD是BC邊上的中線,E是AD的中點,連接BE并延長交AC于點F,G是BF的中點.求證:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com