
 如圖,在△ABC中,點D、E分別在邊AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$
如圖,在△ABC中,點D、E分別在邊AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$分析 (1)由DE∥BC證△ADE∽△ABC得$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,即AE=$\frac{1}{3}$AC,繼而可得$\overrightarrow{AC}$=$\overrightarrow{DC}$-$\overrightarrow{DA}$=$\overrightarrow{b}$-$\overrightarrow{a}$、$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AC}$=$\frac{1}{3}$($\overrightarrow{b}$-$\overrightarrow{a}$),根據$\overrightarrow{DE}$=$\overrightarrow{DA}$+$\overrightarrow{AE}$可得答案;
(2)過點E作EM∥DA、EN∥DC,根據平行四邊形法則即可得.
解答 解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,
∴AE=$\frac{1}{3}$AC,
∵$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,
∴$\overrightarrow{AC}$=$\overrightarrow{DC}$-$\overrightarrow{DA}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∴$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AC}$=$\frac{1}{3}$($\overrightarrow{b}$-$\overrightarrow{a}$),
則$\overrightarrow{DE}$=$\overrightarrow{DA}$+$\overrightarrow{AE}$=$\overrightarrow{a}$+$\frac{1}{3}$($\overrightarrow{b}$-$\overrightarrow{a}$)=$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$;
(2)如圖,過點E作EM∥DA交DC于M,作EN∥DC交DA于點N,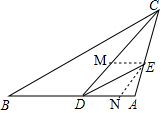
則$\overrightarrow{DM}$、$\overrightarrow{DN}$是向量$\overrightarrow{DE}$在$\overrightarrow{a}$、$\overrightarrow{b}$方向上的分向量.
點評 此題考查了平面向量的知識以及平行四邊形的性質.注意掌握平行四邊形法則與三角形法則的應用是解此題的關鍵.


 每課必練系列答案
每課必練系列答案科目:初中數學 來源: 題型:選擇題
 如圖所示,兩個反比例函數y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限內的圖象依次是C1和C2,設點P在C1上,PC⊥x軸于點C,交C2于點A,PD⊥y軸于點D,交C2于點B,則四邊形PAOB的面積為( )
如圖所示,兩個反比例函數y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限內的圖象依次是C1和C2,設點P在C1上,PC⊥x軸于點C,交C2于點A,PD⊥y軸于點D,交C2于點B,則四邊形PAOB的面積為( )| A. | k1+k2 | B. | k1-k2 | C. | k1•k2 | D. | k1•k2-k2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 第一、二象限 | B. | 第二、四象限 | C. | 第二、三象限 | D. | 第一、三象限 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,OB是∠AOC的平分線,OD是∠COE的平分線,如果∠AOB=40°,∠COE=60°,則∠BOD的度數為( )
如圖,OB是∠AOC的平分線,OD是∠COE的平分線,如果∠AOB=40°,∠COE=60°,則∠BOD的度數為( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知點A在數軸上對應的數為a,點B對應的數為b,且點O為數軸上的原點,|a+5|+(a+b+1)2=0
如圖,已知點A在數軸上對應的數為a,點B對應的數為b,且點O為數軸上的原點,|a+5|+(a+b+1)2=0查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
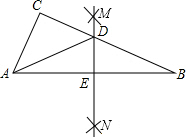 如圖,在△ABC中,分別以點A和點B為圓心,大于$\frac{1}{2}$AB長為半徑畫弧,兩弧交于點M、N,過點M、N作直線交BC于點D,交AB于點E,連接AD.若△ABC的周長為16,△ACD的周長為9,那么線段AE的長是( )
如圖,在△ABC中,分別以點A和點B為圓心,大于$\frac{1}{2}$AB長為半徑畫弧,兩弧交于點M、N,過點M、N作直線交BC于點D,交AB于點E,連接AD.若△ABC的周長為16,△ACD的周長為9,那么線段AE的長是( )| A. | 3.5 | B. | 5 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0.5}\\{y=-7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
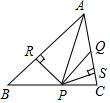 如圖,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三個結論:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如圖,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三個結論:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )| A. | 全部正確 | B. | 僅①正確 | C. | 僅①、②正確 | D. | 僅①、③正確 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com