
 如圖,已知點A在數軸上對應的數為a,點B對應的數為b,且點O為數軸上的原點,|a+5|+(a+b+1)2=0
如圖,已知點A在數軸上對應的數為a,點B對應的數為b,且點O為數軸上的原點,|a+5|+(a+b+1)2=0分析 (1)由絕對值和偶次方的非負性即可求出a、b值;
(2)根據AB=9可知點C在點A的左側或點B的右側,分點C在點A左側和點C在點B右側兩種情況考慮,找出AC、BC的長度結合AC+BC=15即可得出關于x的一元一次方程,解之即可得出結論;
(3)根據點P、Q的運動找出OP、OQ的長度,結合OP=2OQ即可得出關于t的含絕對值符號的一元一次方程,解之即可得出結論.
解答 解:(1)∵|a+5|+(a+b+1)2=0,
∴a+5=0,a+b+1=0,
∴a=-5,b=4.
(2)設點C在數軸上對應的數為x,
∵AB=4-(-5)=9,
∴點C在點A的左側或點B的右側,如圖1所示.
若點C在點A左側,則AC=-5-x,BC=4-x,
∴AC+BC=-5-x+4-x=-1-2x=15,
解得:x=-8;
若點C在點B右側,則AC=x-(-5)=x+5,BC=x-4,
∴AC+BC=x+5+x-4=15,
解得:x=7.
∴點C在數軸上對應的數為-8或7.
(3)OP=|5-2t|,OQ=|4-4t|,如圖2所示.
∵OP=2OQ,
∴|5-2t|=2|4-4t|,
解得:t1=$\frac{1}{2}$,t2=$\frac{13}{10}$.
∴當OP=2OQ時,t的值為$\frac{1}{2}$和$\frac{13}{10}$.
點評 本題考查了一元一次方程的應用、兩點間的距離、數軸、絕對值以及偶次方的非負性,根據兩點間的距離結合線段間的關系列出一元一次方程是解題的關鍵.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:初中數學 來源: 題型:填空題
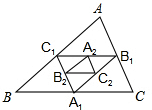 如圖,在△ABC中,A1、B1、C1分別是BC、CA、AB的中點,A2、B2、C2分別是B1C1、C1A1、A1B1的中點,…,An、Bn、Cn分別是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中點,假設△ABC的周長為a,則△A1B1C1的周長為$\frac{1}{2}$a,△A2B2C2的周長為$\frac{1}{4}$a,…,△AnBnCn的周長為$\frac{1}{{2}^{n}}$a.
如圖,在△ABC中,A1、B1、C1分別是BC、CA、AB的中點,A2、B2、C2分別是B1C1、C1A1、A1B1的中點,…,An、Bn、Cn分別是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中點,假設△ABC的周長為a,則△A1B1C1的周長為$\frac{1}{2}$a,△A2B2C2的周長為$\frac{1}{4}$a,…,△AnBnCn的周長為$\frac{1}{{2}^{n}}$a.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
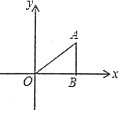 如圖.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,將△ABO繞O點逆時計旋轉90°后得到△A1B1O,則點A1的坐標為( )
如圖.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,將△ABO繞O點逆時計旋轉90°后得到△A1B1O,則點A1的坐標為( )| A. | (-1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$)或(-$\sqrt{3}$,-1) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
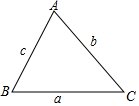
 如圖,在△ABC中,點D、E分別在邊AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$
如圖,在△ABC中,點D、E分別在邊AB、AC上,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在銳角三角形中,
如圖,在銳角三角形中,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
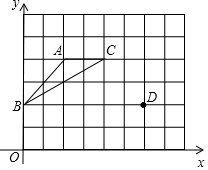 如圖,在坐標系的第一象限建立網格,網格中的每個小正方形邊長都為1,格點△ABC的頂點坐標分別為A(2,4)、B(0,2)、C(4,4).
如圖,在坐標系的第一象限建立網格,網格中的每個小正方形邊長都為1,格點△ABC的頂點坐標分別為A(2,4)、B(0,2)、C(4,4).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 340+$\frac{2}{5}$ | B. | 340×(1+$\frac{2}{5}$) | C. | 340+340×$\frac{3}{5}$ | D. | 340×$\frac{2}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com