Question

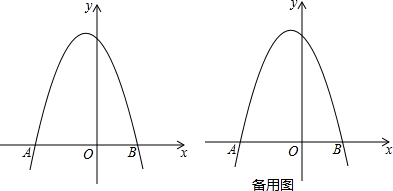
18．如圖△ABC中，∠ACB=90°，AC+BC=8，分別以AB、AC、BC為半徑作半圓，若記圖中陰影部分的面積為y，AC為x，則下列y關于x的圖象中正確的是（　　）

• A．
• B．
• C．
• D．

Answer 1

分析 由圖示知，S_陰影=以AC為直徑的扇形的面積+以BC為直徑的扇形面積-以AB為直徑的扇形面積+△ABC的面積．據此列出y與x的函數關系式，根據函數關系式選擇相應的圖象．

解答 解：∵AC+BC=8，AC=x，
∴BC=8-x．
又∵在△ABC中，∠ACB=90°，
∴AB=$\sqrt{{x}^{2}+（8-x）^{2}}$．
∴S_陰影=$\frac{1}{2}$π×（$\frac{x}{2}$）²+$\frac{1}{2}$π×（$\frac{8-x}{2}$）²-$\frac{1}{2}$π×（$\frac{\sqrt{{x}^{2}+（8-x）^{2}}}{2}$）²+$\frac{1}{2}$x（8-x）=$\frac{1}{2}$x²+4x，
即y=-$\frac{1}{2}$x²+4x（0＜x＜8）．
則該函數圖象是開口向下的拋物線，且自變量的取值范圍是0＜x＜8．
故選：A．

點評 本題考查動點問題的函數圖象、勾股定理，熟知在任何一個直角三角形中，兩條直角邊長的平方之和一定等于斜邊長的平方是解答此題的關鍵．