

���� ��1�������C����ACD=��BCE����SAS�C����ACD�ա�BCE���ɣ��ڸ���(j��)ȫ���������C����ADC=��BEC�������ADC=120�㣬�ó���BEC=120�㣬�Ķ��C����AEB=60�㣻
��2���C����ACD�ա�BCE���ó���ADC=��BEC������C��DM=ME=CM���ɣ�
��� ��1�����C�����ߡ�ACB�͡�DCE�����߅�����Σ�
��CA=CB��CD=CE����ACB=��DCE=60�㣬
���ACD=60��-��CDB=��BCE��
�ڡ�ACD�͡�BCE�У�$\left\{\begin{array}{l}{AC=BC}&{\;}\\{��ACD=��BCE}&{\;}\\{CD=CE}&{\;}\end{array}\right.$��
���ACD�ա�BCE��SAS����
�ڽ⣺�ߡ�ACD�ա�BCE��
���ADC=��BEC��
�ߡ�DCE���߅�����Σ�
���CDE=��CED=60�㣮
���cA��D��E��ͬһֱ���ϣ�
���ADC=120�㣬
���BEC=120�㣮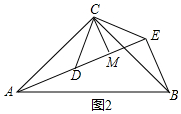
���AEB=��BEC-��CED=60�㣮
��2���⣺��AEB=90�㣬AE=BE+2CM���������£�
��D2��ʾ���ߡ�ACB�͡�DCE�������ֱ�������Σ�
��CA=CB��CD=CE����ACB=��DCE=90�㣮
���ACD=��BCE��
�ڡ�ACD�͡�BCE�У�$\left\{\begin{array}{l}{CA=CB}&{\;}\\{��ACD=��BCE}&{\;}\\{CD=CE}&{\;}\end{array}\right.$��
���ACD�ա�BCE��SAS����
��AD=BE����ADC=��BEC��
�ߡ�DCE�����ֱ�������Σ�
���CDE=��CED=45�㣮
���cA��D��E��ͬһֱ���ϣ�
���ADC=135�㣬
���BEC=135�㣮
���AEB=��BEC-��CED=90�㣮
��CD=CE��CM��DE��
��DM=ME��
�ߡ�DCE=90�㣬
��DM=ME=CM��
��AE=AD+DE=BE+2CM��
�c�u ���}�������ξC���}Ŀ�������˵�߅�����ε��ж��c���|(zh��)��ȫ�������ε��ж��c���|(zh��)������ֱ�������ε��ж��c���|(zh��)��֪�R�����}�C���ԏ�����һ���y�ȣ��쾚���յ�߅�����ε��ж��c���|(zh��)���C��������ȫ���ǽ�Q���}���P�I��



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
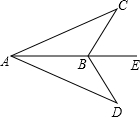 ��֪����D���cB��AE�ϣ���CBA=��DBA��Ҫʹ��ABC�ա�ABD��߀������һ���l����BC=BD���������J���m��?sh��)�һ���l�����ɣ���
��֪����D���cB��AE�ϣ���CBA=��DBA��Ҫʹ��ABC�ա�ABD��߀������һ���l����BC=BD���������J���m��?sh��)�һ���l�����ɣ����鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
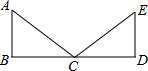 ��D����֪AB��BD��AB��ED��AB=ED��Ҫ�f����ABC�ա�EDC�����ԡ�SAS��������(j��)��߀Ҫ���ӵėl����BC=CD�������ӗl����ACB=��ECD���t������AAS�������������ж�ȫ�ȣ�
��D����֪AB��BD��AB��ED��AB=ED��Ҫ�f����ABC�ա�EDC�����ԡ�SAS��������(j��)��߀Ҫ���ӵėl����BC=CD�������ӗl����ACB=��ECD���t������AAS�������������ж�ȫ�ȣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
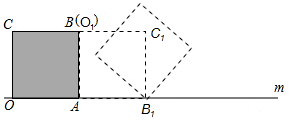 ��߅�L��1�������μ�ƬPABC����ֱ��m�ϣ�OA߅��ֱ��m�ϣ�Ȼ�������μ�Ƭ�@����cA��형rᘷ������D(zhu��n)90�㣬�˕r���cO�\�ӵ����cO1̎�����cB̎�����cC�\�ӵ����cC1̎���cB�\�ӵ����cB1̎���������μ�ƬAO1C1B1�@B1�c����형rᘷ������D(zhu��n)90�㡭��������������(j��ng)�^2016�����D(zhu��n)����cO��(j��ng)�^�Ŀ�·�����L�飨252$\sqrt{2}$+504���У�
��߅�L��1�������μ�ƬPABC����ֱ��m�ϣ�OA߅��ֱ��m�ϣ�Ȼ�������μ�Ƭ�@����cA��형rᘷ������D(zhu��n)90�㣬�˕r���cO�\�ӵ����cO1̎�����cB̎�����cC�\�ӵ����cC1̎���cB�\�ӵ����cB1̎���������μ�ƬAO1C1B1�@B1�c����형rᘷ������D(zhu��n)90�㡭��������������(j��ng)�^2016�����D(zhu��n)����cO��(j��ng)�^�Ŀ�·�����L�飨252$\sqrt{2}$+504���У��鿴�𰸺ͽ���>>
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com