Question

19．如圖①，OA=2，OB=4，以A點(diǎn)為頂點(diǎn)、AB為腰在第三象限作等腰直角△ABC．
（1）點(diǎn)C的坐標(biāo)為（-6，-2）；
（2）如圖②，P是y軸負(fù)半軸上一個(gè)動(dòng)點(diǎn)，當(dāng)P點(diǎn)向y軸負(fù)半軸向下運(yùn)動(dòng)時(shí)，若以P為直角頂點(diǎn)，PA為腰作等腰直角△APD，過點(diǎn)D作DE⊥x軸于點(diǎn)E，則OP-DE的值為2；
（3）如圖③，已知點(diǎn)F坐標(biāo)為（-4，-4），當(dāng)G在y軸運(yùn)動(dòng)時(shí)，作等腰直角△FGH，并始終保持∠GFH=90°，F(xiàn)G與y軸交于點(diǎn)G（0，m），F(xiàn)H與x軸交于點(diǎn)H（n，0），則m與n的關(guān)系為m+n=-8．

Answer 1

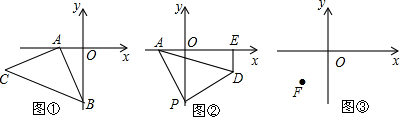
分析 （1）要求點(diǎn)C的坐標(biāo)，則求C的橫坐標(biāo)與縱坐標(biāo)，因?yàn)锳C=AB，則作CM⊥x軸，即求CM和AM的值，容易得△MAC≌△OBA，根據(jù)已知即可求得C點(diǎn)的值；
（2）求OP-DE的值，則將其放在同一直線上，過D作DQ⊥OP于Q點(diǎn)，即是求PQ的值，由圖易求得△AOP≌△PDQ（AAS），即可求得PQ的長；
（3）根據(jù)（2）的結(jié)論，可知m+n為定長，過F分別作x軸和y軸的垂線，運(yùn)用（2）中的方法即可求得m+n的值．

解答 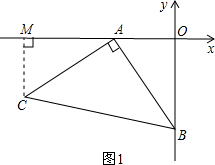解：（1）如圖1，過C作CM⊥x軸于M點(diǎn)，
∵CM⊥OA，AC⊥AB，
∴∠MAC+∠OAB=90°，∠OAB+∠OBA=90°，
∴∠MAC=∠OBA，
在△MAC和△OBA中，
$\left\{\begin{array}{l}{∠CMA=∠AOB=90°}\\{∠MAC=∠OBA}\\{AC=BA}\end{array}\right.$，
∴△MAC≌△OBA（AAS），
∴CM=OA=2，MA=OB=4，
∴OM=6，
∴點(diǎn)C的坐標(biāo)為（-6，-2），
故答案為（-6，-2）；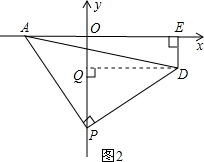

（2）如圖2，過D作DQ⊥OP于Q點(diǎn)，則四邊形OEDQ是矩形，
∴DE=OQ，
∵∠APO+∠QPD=90°，∠APO+∠OAP=90°，
∴∠QPD=∠OAP，
在△AOP和△PDQ中
$\left\{\begin{array}{l}{∠AOP=∠PQD=90°}\\{∠QPD=∠OAP}\\{AP=PD}\end{array}\right.$，
∴△AOP≌△PDQ（AAS），
∴AO=PQ=2，
∴OP-DE=OP-OQ=PQ=OA=2，
故答案為：2；

（3）m+n=-8．
理由：如圖3，過點(diǎn)F分別作FS⊥x軸于S點(diǎn)，F(xiàn)T⊥y軸于T點(diǎn)，則∠HSF=∠GTF=90°=∠SOT，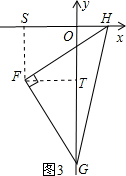
∴四邊形OSFT是正方形，
∴FS=FT=4，∠EFT=90°=∠HFG，
∴∠HFS=∠GFT，
在△FSH和△FTG中，
$\left\{\begin{array}{l}{∠HSF=∠GTF}\\{∠HFS=∠GFT}\\{HF=GF}\end{array}\right.$，
∴△FSH≌△FTG（AAS），
∴GT=HS，
又∵G（0，m），H（n，0），點(diǎn)F坐標(biāo)為（-4，-4），
∴OT═OS=4，
∴GT=-4-m，HS=n-（-4）=n+4，
∴-4-m=n+4，
∴m+n=-8．
當(dāng)點(diǎn)H在點(diǎn)S的左側(cè)，點(diǎn)G在點(diǎn)T的上方時(shí)，
同理可得△FSH≌△FTG，
∴GT=HS，
又∵G（0，m），H（n，0），點(diǎn)F坐標(biāo)為（-4，-4），
∴OT═OS=4，
∴GT=m-（-4）=m+4，HS=n-（-4）=-4-n，
∴-4-n=m+4，
∴m與n的關(guān)系為m+n=-8．
故答案為：m+n=-8．

點(diǎn)評(píng) 本題屬于三角形綜合題，主要考查了三角形全等的判定和性質(zhì)，矩形、正方形的性質(zhì)的綜合應(yīng)用．解決問題的關(guān)鍵是作輔助線構(gòu)造全等三角形，根據(jù)全等三角形的對(duì)應(yīng)邊相等進(jìn)行計(jì)算求解，解題時(shí)注意數(shù)形結(jié)合思想的運(yùn)用．