
 如圖,⊙O的半徑為r.A,B為⊙O上的兩個不同點;以B為圓心.BA為半徑的圓交⊙O于另一點C.P為⊙O內一點,使得△PAB為正三角形,CP交⊙O于另一點Q.
如圖,⊙O的半徑為r.A,B為⊙O上的兩個不同點;以B為圓心.BA為半徑的圓交⊙O于另一點C.P為⊙O內一點,使得△PAB為正三角形,CP交⊙O于另一點Q.分析 (1)假設點P在⊙O上,求此時的正三角形的邊長PB=$\sqrt{3}$r,但已知中“P為⊙O內一點”,所以AB=PB<$\sqrt{3}$r;
(2)本題介紹兩種解法:
解法一:如圖2,作輔助線,證明△POQ是等腰三角形即可得出結論.
解法二:如圖3,作輔助線,證明△OQA是等邊三角形,則OQ=QA,根據四點共圓中,圓外角等于內對角得:∠MAB=∠BCQ=∠BPC,根據平角的定義求得:∠QPA=∠QAP,所以QP=QA,由等量代換可以得出結論QP=OQ=r.
解答 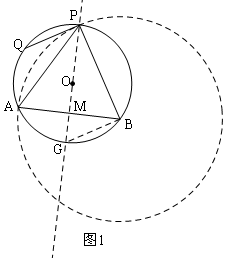 證明:(1)如圖1,當P在圓O上時,過O作OG⊥AB于M,交⊙O于G,連接BG,
證明:(1)如圖1,當P在圓O上時,過O作OG⊥AB于M,交⊙O于G,連接BG,
∴AM=BM,
∴GO是AB的中垂線,
∵△PAB是正三角形,
∴PA=PB=AB,∠PAB=60°,
∴P在GO上,
∴GP是⊙O的直徑,
∴∠GBP=90°,
∵∠PGB=∠PAB=60°,
在Rt△PGB中,GP=2r,
sin60°=$\frac{PB}{GP}$=$\frac{\sqrt{3}}{2}$
$\frac{PB}{2r}$=$\frac{\sqrt{3}}{2}$,
PB=$\sqrt{3}$r,
∵P為⊙O內一點,
∴AB=PB<$\sqrt{3}$r;
(2)解法一:如圖2,連接OQ、OA、OB、AC、BC,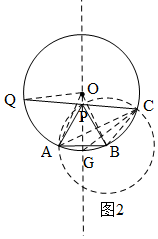
在⊙O中,∠PCA=$\frac{1}{2}$∠PBA=30°,
∵△PAB為等邊三角形,
∴∠GPB=∠GPA=$\frac{1}{2}$∠APB=30°,
∵OA=OB,OG⊥AB,
∴∠AOG=$\frac{1}{2}$∠AOB,
在⊙O中,∠QOG=∠QOA+∠AOG,
=2∠QCA+∠AOG,
=60°+$\frac{1}{2}$∠AOB,
∵∠PCA=30°,∠GPB=30°,
∴∠QOG=∠PCA+∠GPB+∠ACB=∠GPB+∠PCB,
∵BP=BC,
∴∠BPC=∠BCP,
∴∠QOG=∠GPB+∠BPC=∠GPC=∠QPO,
∴PQ=OQ=r.
解法二:如圖3,連接AC、OA、AQ、OQ、BC,延長QA交⊙B于M,
得:∠PCA=$\frac{1}{2}$∠PBA=30°,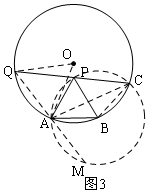
∠O=2∠PCA=2∠QCA=60°,
∴△OQA是等邊三角形,
∴OQ=QA,
∵Q、A、B、C四點共圓,
∴∠MAB=∠BCQ=∠BPC,
∵∠QPA=180°-60°-∠BPC=120°-∠BPC,
∠QAP=180°-60°-∠MAB=120°-∠BPC,
∴∠QPA=∠QAP,
∴QP=QA,
∴QP=OQ=r.
點評 本題是圓的綜合題,考查了圓周角定理、等邊三角形的性質、等腰三角形的判定、特殊的三角函數的問題,第一問中確定動點A、B運動時,AB的長度的變化范圍,第二問中確定PQ與中間量半徑的關系是關鍵,從而使問題得以解決.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
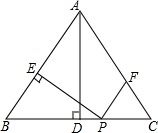 如圖,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于點D,動點P從點B出發沿BC方向以每秒5個單位的速度向終點C運動,過點P作PE⊥AB于點E,過點P作PF∥BA,交AC于點F,設點P運動的時間為t秒,若以PE所在直線為對稱軸,線段BD經軸對稱變換后的圖形為B′D′,當線段B′D′與線段AC有公共點時,則t的取值范圍是$\frac{5}{6}$≤t≤$\frac{61}{60}$.
如圖,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于點D,動點P從點B出發沿BC方向以每秒5個單位的速度向終點C運動,過點P作PE⊥AB于點E,過點P作PF∥BA,交AC于點F,設點P運動的時間為t秒,若以PE所在直線為對稱軸,線段BD經軸對稱變換后的圖形為B′D′,當線段B′D′與線段AC有公共點時,則t的取值范圍是$\frac{5}{6}$≤t≤$\frac{61}{60}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
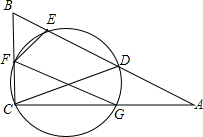 如圖,D為Rt△ABC斜邊AB上一點,以CD為直徑的圓分別交△ABC三邊于E、F、G三點,連接FE,FG.
如圖,D為Rt△ABC斜邊AB上一點,以CD為直徑的圓分別交△ABC三邊于E、F、G三點,連接FE,FG.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
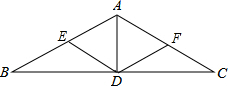 如圖,在△ABC中,AB=AC,∠BAC=120°,AD是BC邊的中線,點E、F分別是AB、AC的中點,連接DE、DF.
如圖,在△ABC中,AB=AC,∠BAC=120°,AD是BC邊的中線,點E、F分別是AB、AC的中點,連接DE、DF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知,如圖△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,與CD相交于點F,求證:①BF=AC;②BF=2CE.
已知,如圖△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,與CD相交于點F,求證:①BF=AC;②BF=2CE.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
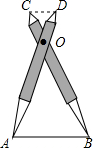 如圖,比例規是一種畫圖工具,它由長度相等的兩腳AD和BC交叉構成,利用它可以把線段按一定的比例伸長或縮短,如果把比例規的兩腳合上,使螺絲釘固定在刻度3的地方(即同時使OA=3OD,OB=3OC),然后張開兩腳,使A、B兩個尖端分別在線段l的兩個端點上,若CD=3.2cm,則AB的長為9.6cm.
如圖,比例規是一種畫圖工具,它由長度相等的兩腳AD和BC交叉構成,利用它可以把線段按一定的比例伸長或縮短,如果把比例規的兩腳合上,使螺絲釘固定在刻度3的地方(即同時使OA=3OD,OB=3OC),然后張開兩腳,使A、B兩個尖端分別在線段l的兩個端點上,若CD=3.2cm,則AB的長為9.6cm.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com