
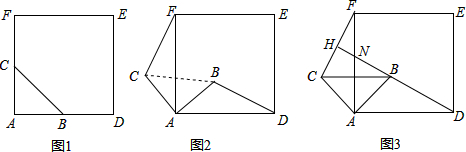
 課本上有這樣一道題目:
課本上有這樣一道題目:分析 (1)由于AB=AC,∠BAC=90°,從而求出∠B=∠ACB=45°,又因為BD=BA,可知∠BAD=∠BDA=67.5°,因為CE=CA,可知∠CAE=∠E=$\frac{1}{2}$∠ACB=22.5°,最后可求出得∠DAE=∠BAE-∠BAD=45°.
(2)可設∠CAE=x,從而可知∠E=x,∠ACB=2x,∠B=90°-∠ACB=90°-2x,然后可求出∠BAD=∠BDA=x+45°,∠BAE=90°+x,所以∠DAE=∠BAE-∠BAD=(90°+x)-(x+45°)=45°,
(3)可設∠CAE=x,∠BAD=y,則∠B=180°-2y,∠E=∠CAE=x,從而可知∠BAE=2y-x,∠DAE=y-x,∠BAC=2y-2x,所以可知∠DAE=$\frac{1}{2}$∠BAC,
解答 解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=$\frac{1}{2}$(180°-∠B)=67.5°,
∵CE=CA
∴∠CAE=∠E=$\frac{1}{2}$∠ACB=22.5°,
∴∠BAE=180°-∠B-∠E=112.5°,
∴∠DAE=∠BAE-∠BAD=45°,
(2)不改變
設∠CAE=x,則∠E=x,∠ACB=2x,
∵∠B=90°-∠ACB=90°-2x,
∴∠BAD=∠BDA=$\frac{1}{2}$(180°-∠B)=x+45°,
∠BAE=180°-∠B-∠E=90°+x,
∴∠DAE=∠BAE-∠BAD=(90°+x)-(x+45°)=45°,
(3)∠DAE=$\frac{1}{2}$∠BAC,
理由:設∠CAE=x,∠BAD=y,
則∠B=180°-2y,∠E=∠CAE=x,
∴∠BAE=180°-∠B-∠E=2y-x,
∴∠DAE=∠BAE-∠BAD=2y-x-y=y-x,
∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x
∴∠DAE=$\frac{1}{2}$∠BAC,
點評 本題考查等腰三角形的性質,解題的關鍵是根據等腰三角形的性質分別求出各角的度數,然后利用度數計算的方法求出∠DAE與∠BAC的關系,本題屬于中等題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
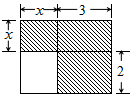 下面四個整式中,不能表示圖中陰影部分面積的是( )
下面四個整式中,不能表示圖中陰影部分面積的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=2(x+1)2-2 | B. | y=2(x-1)2-2 | C. | y=2(x-2)2-1 | D. | y=2(x+2)2+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com