

分析 (1)①根據(jù)等腰直角三角形的性質(zhì)得到∠B=∠C=45°,證明∠BAP=∠QPC,根據(jù)相似三角形的判定定理證明結(jié)論;
②分AP=AQ、AP=PQ和AQ=PQ三種情況,根據(jù)等腰三角形的性質(zhì)、相似三角形的性質(zhì)解答;
(2)根據(jù)等腰三角形的性質(zhì)和相似三角形的判定定理證明△CAP∽△PAD,根據(jù)相似三角形的性質(zhì)計算即可;
(3)根據(jù)三角形內(nèi)角和定理進行判斷即可.
解答 解:(1)①∵∠BAC=90°,AB=AC=2,
∴∠B=∠C=45°,
∵∠BAP+∠APB=135°,
∠APB+∠QPC=135°,
∴∠BAP=∠QPC,
∴△ABP∽△PCQ;
②當(dāng)AP=AQ時,∠APQ=∠AQP=45°,
∴∠PAQ=90°,
∴點P與點B、點Q與點C重合,不合題意;
當(dāng)AP=PQ時,∵△ABP∽△PCQ,
∴△ABP≌△PCQ,
∴AB=PC=2,
∴BP=CQ=2$\sqrt{2}$-2,
∴AQ=AC-CQ=4-2$\sqrt{2}$;
當(dāng)AQ=PQ時,∠PAQ=∠APQ=45°,
∴∠APC=∠AQP=90°,
∴AQ=PQ=QC=1;
(2)存在,
∵∠ACB=90°,
∴∠CAP+∠APC=45°,
∵∠APQ=45°,
∴∠CAP+∠D=45°,
∴∠APC=∠D,
∴△CAP∽△PAD,
∴$\frac{AC}{AP}$=$\frac{PC}{PD}$,又AP=PD,
∴PC=AC=2;
(3)不存在,
∵P和B不重合,
∴∠PAQ>90°,
∴∠APQ=45°,∠AQP<45°,
∴AP≠AQ.
點評 本題考查的是相似三角形的判定和性質(zhì)、等腰三角形的判定和性質(zhì),掌握相關(guān)的性質(zhì)定理、靈活運用分情況討論思想是解題的關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:解答題
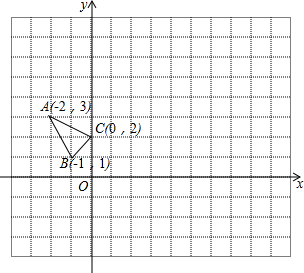 △ABC在平面直角坐標(biāo)系中的位置如圖所示.
△ABC在平面直角坐標(biāo)系中的位置如圖所示.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,在四邊形ABCD中,AC=AD,∠CAD=α,在CB邊上取一點E,使∠DEB與∠DAC互補,探究線段AE、DE、CE的數(shù)量關(guān)系.
如圖,在四邊形ABCD中,AC=AD,∠CAD=α,在CB邊上取一點E,使∠DEB與∠DAC互補,探究線段AE、DE、CE的數(shù)量關(guān)系.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,將△ABC繞點A逆時針旋轉(zhuǎn)一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,則∠BAC的度數(shù)為85°.
如圖,將△ABC繞點A逆時針旋轉(zhuǎn)一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,則∠BAC的度數(shù)為85°.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
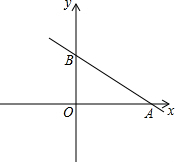 如圖,在直角坐標(biāo)系xOy中,O為坐標(biāo)原點,直線y=kx-$\sqrt{3}$k+3交y軸正半軸于點B,交x軸于點A.
如圖,在直角坐標(biāo)系xOy中,O為坐標(biāo)原點,直線y=kx-$\sqrt{3}$k+3交y軸正半軸于點B,交x軸于點A.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 在△ABC中,AB=AC,BD為△ABC的高,如果∠BAC=40°,則∠CBD的度數(shù)是( )
在△ABC中,AB=AC,BD為△ABC的高,如果∠BAC=40°,則∠CBD的度數(shù)是( )| A. | 70° | B. | 40° | C. | 20° | D. | 30° |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com