
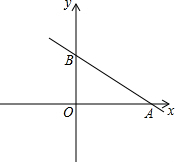
 如圖,在直角坐標系xOy中,O為坐標原點,直線y=kx-$\sqrt{3}$k+3交y軸正半軸于點B,交x軸于點A.
如圖,在直角坐標系xOy中,O為坐標原點,直線y=kx-$\sqrt{3}$k+3交y軸正半軸于點B,交x軸于點A.分析 (1)根據(jù)已知條件得到當x=$\sqrt{3}$時,y=k×$\sqrt{3}$-$\sqrt{3}$k+3=3,即可得到結(jié)論;
(2)①當OC⊥AB時,點O到直線AB的距離最大,如圖1,過點C任作一條異于直線AB的直線DE,并過點O作OF⊥DE于點F,則在Rt△△OCF中,斜邊OC>OF,于是得到當點C與F重合,即OC⊥AB時,點O到直線AB的距離最大,此時OC=$\sqrt{(0-\sqrt{3})^{2}+(0-3)^{2}}$=2$\sqrt{3}$,如圖2,過點C作CD⊥x軸于點D,由C($\sqrt{3}$,3),則∠COD=60°在Rt△AOC中,∠CAO=30°,OC=2$\sqrt{3}$,求得OA=4$\sqrt{3}$,得到A(4$\sqrt{3}$,0),代入即可得到結(jié)論;
②當∠OBP=90°時,如圖3,(Ⅰ)若△BOP∽△BAO,則∠BOP=∠BAO=30°,解直角三角形得到BP=$\frac{\sqrt{3}}{3}$OB=$\frac{4\sqrt{3}}{3}$,求得P2($\frac{4\sqrt{3}}{3}$,4),(Ⅱ)若△BPO∽△BAO,則∠BPO=∠BAO=30°,解直角三角形得到BP=$\sqrt{3}$OB=4$\sqrt{3}$,求得P1(4$\sqrt{3}$,4);當∠OPB=90°時(Ⅲ)過點P作OP⊥BA于點P,如圖4,此時△PBO∽△OBA,∠BOP=∠BAO=30°過點P作PM⊥OA于點M.在Rt△PBO中,根據(jù)直角三角形的性質(zhì)得到BP=$\frac{1}{2}$OB=2,OP=$\sqrt{3}$BP=2$\sqrt{3}$,在Rt△PMO中,∠OPM=30°,根據(jù)直角三角形的性質(zhì)得到OM=$\frac{1}{2}$OP=$\sqrt{3}$,PM=$\sqrt{3}$OM=3,求得P3($\sqrt{3}$,3),(Ⅳ)若△POB∽△OBA,如圖4,則∠OBP=∠BAO=30°,∠POM=30°.解直角三角形得到PM=$\frac{\sqrt{3}}{3}$OM=1,求得P4($\sqrt{3}$,1),當∠POB=90°時,點P在x軸上,不符合要求.
解答 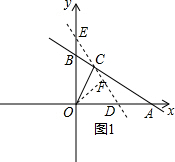 解:(1)依題意,得
解:(1)依題意,得
當x=$\sqrt{3}$時,y=k×$\sqrt{3}$-$\sqrt{3}$k+3=3,
∴點C($\sqrt{3}$,3)一定在直線AB上;
(2)①當OC⊥AB時,點O到直線AB的距離最大,
如圖1,過點C任作一條異于直線AB的直線DE,并過點O作OF⊥DE于點F,
則在Rt△△OCF中,斜邊OC>OF,
∴當點C與F重合,即OC⊥AB時,點O到直線AB的距離最大,
此時OC=$\sqrt{(0-\sqrt{3})^{2}+(0-3)^{2}}$=2$\sqrt{3}$,
如圖2,過點C作CD⊥x軸于點D,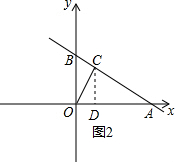
∵C($\sqrt{3}$,3),則∠COD=60°
在Rt△AOC中,∠CAO=30°,OC=2$\sqrt{3}$,
∴OA=4$\sqrt{3}$,圖1
∴A(4$\sqrt{3}$,0),
∴0=4$\sqrt{3}$k-$\sqrt{3}$k+3解得k=-$\frac{\sqrt{3}}{3}$,
∴直線AB的解析式為y=-$\frac{\sqrt{3}}{3}$x+4;
②當∠OBP=90°時,如圖3,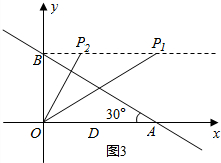 (Ⅰ)若△BOP∽△BAO,
(Ⅰ)若△BOP∽△BAO,
則∠BOP=∠BAO=30°,BP=$\frac{\sqrt{3}}{3}$OB=$\frac{4\sqrt{3}}{3}$,
∴P2($\frac{4\sqrt{3}}{3}$,4),
(Ⅱ)若△BPO∽△BAO,
則∠BPO=∠BAO=30°,BP=$\sqrt{3}$OB=4$\sqrt{3}$,
∴P1(4$\sqrt{3}$,4);
當∠OPB=90°時
(Ⅲ)過點P作OP⊥BA于點P,如圖4,
此時△PBO∽△OBA,∠BOP=∠BAO=30°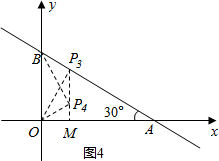
過點P作PM⊥OA于點M.
在Rt△PBO中,BP=$\frac{1}{2}$OB=2,
OP=$\sqrt{3}$BP=2$\sqrt{3}$,
∵在Rt△PMO中,∠OPM=30°,
∴OM=$\frac{1}{2}$OP=$\sqrt{3}$,PM=$\sqrt{3}$OM=3,
∴P3($\sqrt{3}$,3),
(Ⅳ)若△POB∽△OBA,如圖4,
則∠OBP=∠BAO=30°,∠POM=30°.
∴PM=$\frac{\sqrt{3}}{3}$OM=1,
∴P4($\sqrt{3}$,1),
當∠POB=90°時,點P在x軸上,不符合要求.
綜合得,符合條件的點有四個,分別是p2($\frac{4}{3}\sqrt{3}$,4),p1(4$\sqrt{3}$,4),p3($\sqrt{3}$,3),p4($\sqrt{3}$,1).
點評 本題綜合考查了用待定系數(shù)法求一次函數(shù)的解析式和相似三角形的有關(guān)知識,解決這類問題常用到分類討論、數(shù)形結(jié)合、方程和轉(zhuǎn)化等數(shù)學思想方法.


科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 在三個偶數(shù)中任選一個能被2整除 | |
| B. | 兩個有理數(shù)相除,結(jié)果是無理數(shù) | |
| C. | 一個四邊形的內(nèi)角和是560° | |
| D. | 用一個平面去截圓柱體,得到的截面是矩形 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
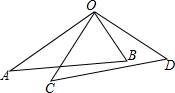 如圖所示,將一副三角板疊放在一起,使直角頂點重合,且∠AOD=2∠BOC,則∠AOC的等于( )
如圖所示,將一副三角板疊放在一起,使直角頂點重合,且∠AOD=2∠BOC,則∠AOC的等于( )| A. | 45° | B. | 30° | C. | 25° | D. | 20° |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 3.14 | C. | $\frac{11}{7}$ | D. | $-\root{3}{0.001}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
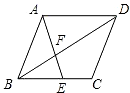 如圖,平行四邊形ABCD中,E是邊BC上的點,AE交BD于點F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.
如圖,平行四邊形ABCD中,E是邊BC上的點,AE交BD于點F,如果$\frac{BE}{EC}=\frac{3}{2}$,那么$\frac{{{S_{△BEF}}}}{{{S_{△DAF}}}}$=$\frac{9}{25}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com