Question

19．閱讀下面材料：
小天在學習銳角三角函數中遇到這樣一個問題：在Rt△ABC中，∠C=90°，∠B=22.5°，則tan22.5°=$\sqrt{2}$-1

小天根據學習幾何的經驗，先畫出了幾何圖形（如圖1），他發現22.5°不是特殊角，但它是特殊角45°的一半，若構造有特殊角的直角三角形，則可能解決這個問題．于是小天嘗試著在CB邊上截取CD=CA，連接AD（如圖2），通過構造有特殊角（45°）的直角三角形，經過推理和計算使問題得到解決．
請回答：tan22.5°=$\sqrt{2}$-1．
參考小天思考問題的方法，解決問題：
如圖3，在等腰△ABC 中，AB=AC，∠A=30°，請借助△ABC，構造出15°的角，并求出該角的正切值．

Answer 1

分析 如圖2，設CD=CA=a，△ACD為等腰直角三角形，則AD=$\sqrt{2}$a，易得∠DAB=∠B=22.5°，所以DB=DA=$\sqrt{2}$a，再在Rt△ABC中，利用正切定義可計算出tanB=$\sqrt{2}$-1，即tan22.5°=$\sqrt{2}$-1；
如圖3，延長BA到D，使AD=AB，則AB=AD=AC，則∠D=∠ACD，利用三角形外角性質易得∠D=15°，作CH⊥AB于H，設CH=x，利用含30度三邊的關系得到AC=2x，AH=$\sqrt{3}$x，則AD=AC=2x，DH=AD+AH=（2+$\sqrt{3}$）x，然后在Rt△DCH中，利用正切的定義可計算出tanD=2-$\sqrt{3}$，即tan15°=2-$\sqrt{3}$．

解答 解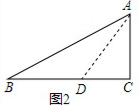：如圖2，設CD=CA=a，則AD=$\sqrt{2}$a，
∵∠B=22.5°，∠ADC=45°，
∴∠DAB=22.5°，
∴∠DAB=∠B，
∴DB=DA=$\sqrt{2}$a，
∴BC=BD+CD=（$\sqrt{2}$+1）a，
在Rt△ABC中，tanB=$\frac{AC}{BC}$=$\frac{a}{（\sqrt{2}+1）a}$=$\sqrt{2}$-1，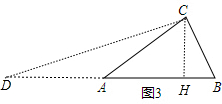
即tan22.5°=$\sqrt{2}$-1；
故答案為$\sqrt{2}$-1；$\sqrt{2}$-1；
如圖3，延長BA到D，使AD=AB，則AB=AD=AC，
∴∠D=∠ACD，
∵∠CAB=∠D+∠ACD=30°，
∴∠D=15°，
作CH⊥AB于H，設CH=x，則AC=2x，AH=$\sqrt{3}$x，
∴AD=AC=2x，
∴DH=AD+AH=（2+$\sqrt{3}$）x，
在Rt△DCH中，tanD=$\frac{CH}{DH}$=$\frac{x}{（2+\sqrt{3}）x}$=2-$\sqrt{3}$，
即tan15°=2-$\sqrt{3}$．

點評 本題考查了解直角三角形：在直角三角形中，由已知元素求未知元素的過程就是解直角三角形．解決本題的關鍵是構建含22.5度和15度的直角三角形．